The centroid of an ice cream cone (spherical box)

Fix  between 0 and .   We want to compute the centroid of the solid  consisting of all points

( )   such that    is between 0 and 1,  is between 0 and , and  is between 0 and .    Here is it's picture for   .

>

>	icc:=(phi0,n)->display(plot3d(1, t=0..2*Pi, p=0..phi0, coords=spherical, style=wireframe,color=blue),seq(line([0,0,0],[sin(phi0)*cos(2*Pi*i/n),sin(phi0)*sin(2*Pi*i/n),cos(phi0)],thickness=2,color=red),i=1..n),scaling=constrained,axes=normal):

>	icc(Pi/4,72);

By inspection, we can see that the centroid is (0,0,a) where a is somewhere between 0 and 1, depending on .    The volume  and moment about the xy-plane  can best be evaluated as  iterated integrals in spherical coordinates.

>	V := Int(Int(Int(1,z),x=S[phi[0]]..``),y)=Int(Int(Int(1*rho^2*(sin(phi)),rho=0..1),phi=0..phi0),theta=0..2*Pi);

Now the volume of the ice cream cone with cone angle  and cone slant height 1 is

>	V := int(int(int(1*rho^2*(sin(phi)),rho=0..1),phi=0..phi0),theta=0..2*Pi);

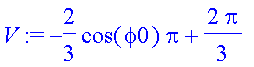
And the moment about the xy plane is

>

>	Mxy := Int(Int(Int(z,z),x=S[phi[0]]..``),y)= Int(Int(Int(rho*cos(phi)*rho^2*sin(phi),rho=0..1),phi=0..phi0),theta=0..2*Pi);

This evaluates to

>	Mxy := int(int(int(rho*cos(phi)*rho^2*sin(phi),rho=0..1),phi=0..phi0),theta=0..2*Pi);

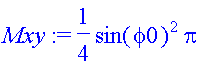
So we can calculate the z-coordinate of the centroid, zbar as

>	zbar:= unapply(Mxy/V,phi0);

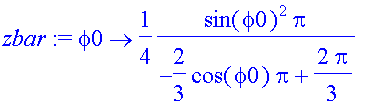
And for example when the cone angle is 90 degrees, zbar is

>	simplify(zbar(Pi/4))=evalf(zbar(Pi/4));

>

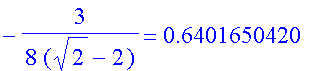
(So we did calculate it incorrectly in class as .75)

We can add the centroid to the picture and check to see if it looks reasonable.

>	picture:= phi0->display(pointplot3d([0,0,evalf(zbar(phi0))],symbol=circle,color=black,thickness=3),icc(phi0,20),scaling=constrained,orientation=[116,80]);

>	picture(Pi/4);

This seems eminately reasonable.  Now lets make a movie of the locus of the centroid of the spherical box as phi[0] goes from 0 to Pi.

>	display(seq(picture(i*Pi/20),i=1..20),scaling=constrained,insequence=true);

As in the case of the centroid of the pie slice, we see that as  approaches  ,  the centroid moves to the center of the ball.  At the other extreme (when phi[0] is getting closer to 0, the ice cream cone is approaching a segment (with centroid at the middle of the segment), but the centroid is approaching a number closer to 1 than 0.  In the case of the pie slice, this number was 2/3, the limit of the centroid of the triangle approximation to the pie slice.  In this case the number is

>	Limit(zbar(t),t=0,right)=limit(zbar(t),t=0,right);

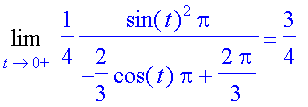
Question:    Why that number?    Perhaps if you solve the problem below, you could come up with an explanation.

Problem:   Calculate the centroid of the cone of  slant height 1 and base radius r.