Greens theorem.
Green's theorem states that if F = <P,Q> has continuous partial derivatives on an open set containing the positively oriented simple closed curve C and the region D it bounds, then the line integral of the the tangential component of F with repect to arc length around C is the double integral over D of the difference
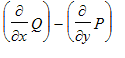 .
.
The left hand side of Green's theorem has a nice meaning: If the integral is positive, then on average the tangential component of F is positive, so if we take the view that F is a velocity flow for a fluid, that says that the net flow of the fluid on the boundary curve C is counterclockwise. If we divide by the length of the curve, we would get average signed speed that a point on the curve is rolled around the curve by the velocity field. If the curve is a small circle of radius r then Green's theorem says that this average angular velocity is approximately one half the above difference of partial derivatives. For this reason the the difference is a measure of the rotational tendency of the velocity field at each point, and as such is called the curl of F.
Note
: The curl of a 3 dimensional velocity field F = <P, Q, R> is the vector Del X F = <
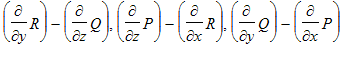 > . If F is 2 dimensional (R = 0) we can call the 3rd component the curl of F.
Stokes theorem
is a generalization of Greens theorem to the situation in space where C is a space curve and D is a surface bounded by C. It says that the line integral of the tangential component of F around C is equal to the surface integral of the normal component of curl F over D.
> . If F is 2 dimensional (R = 0) we can call the 3rd component the curl of F.
Stokes theorem
is a generalization of Greens theorem to the situation in space where C is a space curve and D is a surface bounded by C. It says that the line integral of the tangential component of F around C is equal to the surface integral of the normal component of curl F over D.
If instead of integrating the tangential component of the velocity field F around the curve C, we integrate the normal component of F, we get another line integral which can also be equated to a double integral by Green's theorem. The outward normal n to the curve C is obtained by rotating the tangent vector <dx/dt, dy/dt>/|r'(t)| 90 degrees clockwise to get n = <dy/dt, -dx/dt>/|r'(t)|
The line integral of the normal component of F = <P,Q> then becomes
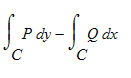 . By Greens theorem this is equal to the the double integral
. By Greens theorem this is equal to the the double integral
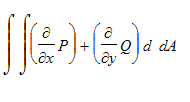 , This is called the
normal form
of Greens theorem. The right hand side of this equation measures the transport of fliud across the curve C (positive means fluid is flowing out on average, negative means fluid is flowing in). The integrand of the right hand integral is called the divergence of the velocity field F. More generally, the divergence of a vector field F = <P,Q,R> is defined as div F = del dot F =
, This is called the
normal form
of Greens theorem. The right hand side of this equation measures the transport of fliud across the curve C (positive means fluid is flowing out on average, negative means fluid is flowing in). The integrand of the right hand integral is called the divergence of the velocity field F. More generally, the divergence of a vector field F = <P,Q,R> is defined as div F = del dot F =
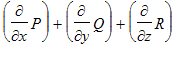 . The
Divergence theorem
is a generalization of the normal form of Green's theorem to the situation in space where you have a surface R bounding a soliid S in space where there is a nice velocity field F defined on an open set containing S and R. It says that the surface integral of the (outward) normal component of F over R is equal to the triple integral of the divergence of F over the solid S.
. The
Divergence theorem
is a generalization of the normal form of Green's theorem to the situation in space where you have a surface R bounding a soliid S in space where there is a nice velocity field F defined on an open set containing S and R. It says that the surface integral of the (outward) normal component of F over R is equal to the triple integral of the divergence of F over the solid S.
procedure 1 to investigate velocity fields: Tangential form of Greens theorem.
integration review
Integration review:
Defintions: Know these and be able to use them.
Riemann sum
Double integral
Area and volume as a double integral
Iterated integral
Type 1 and type 2 regions
Average value of a function on a region
first and second moments (about a line) of a function on a region
center of mass of a lamina, centroid of a region
Radius of gyration of a lamina about the y-axis (x-axis)
Triple integral
Volume as a triple integral
Line integrals with respect to arc length, x, y, or z (if the curve is a space curve)
Length as a line integral
vector field Force field
Work as a line integral
gradient field
conservative vector field
potential
Theorems: Know these and their consequences
Linearity of double integrals (and triple integrals and line integrals).
Comparability of double integrals ( and triple integrals and line integrals)
Fubini's Theorem
Change of variables Theorem
Fundamental Theorem for line integrals
Characterization Theorem for conservative vector fields
Green's Theorem
Typical problems
16_12
Compute a Riemann sum for a function
Compute a Riemann sum for a table of values
Double integral as the limit of a Riemann sum.
Compute a double integral by realizing it as a volume
Use Fubini's Theorem to compute a double integral
Compute an iterated integral
Compute a volume using an iterated integral
Compute an average height
>
16_34
double integral trivia
compute a double integral over a type 1 or type 2
another compute a double integral over a type 1 or type 2
another compute a double integral over a type 1 or type 2
reverse the order of integration
convert to polar coordinates
compute a volume using polar coordinates
What's left after a hole is drilled in a sphere?
>
16_56
compute the center of mass of a triangular region with variable density
Find center of mass of quarter disk
Find radius of gyration of rectangle in first quadrant
compute the area of a plane which lies above a given triangle.
another compute a double integral over a type 1 or type 2
compute an area using polar coordinates
What's left after a hole is drilled in a sphere?
>
16_78
evaluate a triple iterated integral
compute an average temperature
compute an average temperature using cylindrical coordinates
compute a mass using spherical coordinates
y-coordinate of the center of mass.
Find average density of a prism
change of variable problem for double integrals
change of variable problem for triple integrals
17_12
identify a gradient field
Find the area of a fence. Find its average height
Find the mass and center of mass of a wire Find its average density.
Calculate line integrals with respect to x or y
Calculate a work integral along various paths from A to B
>
17_34
Calculate line integrals for gradient fields
Find potentials.
Calculate work integral using Green's theorem
Express area as line integral and evaluate.
Sample questions. More later in week
.
1. Draw a picture of the region R for the integral
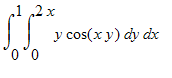 . Then reverse the order of integration and evaluate.
. Then reverse the order of integration and evaluate.
2. Find the average value of
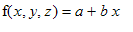 over the rectangular solid with opposite corners (0,0,0) and (1,2,3)
over the rectangular solid with opposite corners (0,0,0) and (1,2,3)
3. Let a > 0. Let
![H[a]](images/integraion_review10.gif) be the solid below the plane
be the solid below the plane
 , above the xy-plane and inside the cylinder
, above the xy-plane and inside the cylinder
 . Express the volume of
. Express the volume of
![H[a]](images/integraion_review13.gif) as an iterated double integral in polar coordinates. Evaluate. Calculate the centroid of
as an iterated double integral in polar coordinates. Evaluate. Calculate the centroid of
![H[a]](images/integraion_review14.gif) .
.
4. Find the maximum and minimum values M and m of
 on the domain D = {(x,y)|
on the domain D = {(x,y)|
 }. Then show that the integral of f over D is between
}. Then show that the integral of f over D is between
 and
and

5. Find the center of mass of the line segment from (0,1,0) to (2,0,1) if the density at each point on the wire is given by
 .
.
6. Show that the vector field F =<P,Q> = <
 > is conservative. Use this to evaluate the work integral
> is conservative. Use this to evaluate the work integral
 . over any nice curve C from (0,0) to (1,1).
. over any nice curve C from (0,0) to (1,1).
7. Obtain the formula for the area of a triangle with base b and height h by evaluating a line integral
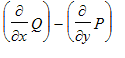 .
.
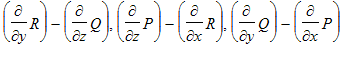 > . If F is 2 dimensional (R = 0) we can call the 3rd component the curl of F.
Stokes theorem
is a generalization of Greens theorem to the situation in space where C is a space curve and D is a surface bounded by C. It says that the line integral of the tangential component of F around C is equal to the surface integral of the normal component of curl F over D.
> . If F is 2 dimensional (R = 0) we can call the 3rd component the curl of F.
Stokes theorem
is a generalization of Greens theorem to the situation in space where C is a space curve and D is a surface bounded by C. It says that the line integral of the tangential component of F around C is equal to the surface integral of the normal component of curl F over D.
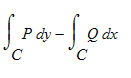 . By Greens theorem this is equal to the the double integral
. By Greens theorem this is equal to the the double integral
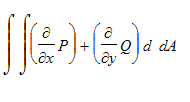 , This is called the
normal form
of Greens theorem. The right hand side of this equation measures the transport of fliud across the curve C (positive means fluid is flowing out on average, negative means fluid is flowing in). The integrand of the right hand integral is called the divergence of the velocity field F. More generally, the divergence of a vector field F = <P,Q,R> is defined as div F = del dot F =
, This is called the
normal form
of Greens theorem. The right hand side of this equation measures the transport of fliud across the curve C (positive means fluid is flowing out on average, negative means fluid is flowing in). The integrand of the right hand integral is called the divergence of the velocity field F. More generally, the divergence of a vector field F = <P,Q,R> is defined as div F = del dot F =
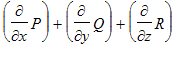 . The
Divergence theorem
is a generalization of the normal form of Green's theorem to the situation in space where you have a surface R bounding a soliid S in space where there is a nice velocity field F defined on an open set containing S and R. It says that the surface integral of the (outward) normal component of F over R is equal to the triple integral of the divergence of F over the solid S.
. The
Divergence theorem
is a generalization of the normal form of Green's theorem to the situation in space where you have a surface R bounding a soliid S in space where there is a nice velocity field F defined on an open set containing S and R. It says that the surface integral of the (outward) normal component of F over R is equal to the triple integral of the divergence of F over the solid S.
![[Maple Plot]](images/integraion_review6.gif)
![[Maple Plot]](images/integraion_review7.gif)
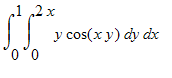 . Then reverse the order of integration and evaluate.
. Then reverse the order of integration and evaluate.
 . Express the volume of
. Express the volume of
 on the domain D = {(x,y)|
on the domain D = {(x,y)|
 }. Then show that the integral of f over D is between
}. Then show that the integral of f over D is between
 > is conservative. Use this to evaluate the work integral
> is conservative. Use this to evaluate the work integral
 . over any nice curve C from (0,0) to (1,1).
. over any nice curve C from (0,0) to (1,1).