Exercise 1 . Let l and m be the lines with equations and respectively. Find the point P of intersection of l and m. Let A = [2,7] and B = [0,b]. Find b so that P is on the line through A and B.

> l := 3*x + 2*y = 12;
m := 4*x + y = 10;

> sol := solve({l,m},{x,y});

> P := subs(sol,[x,y]);

> A := [2,7];
B := [0,b];

> sol2 :=solve((b-A[2])/(B[1]-A[1])=(P[2]-A[2])/(P[1]-A[1]),{b});

The notion of distance between two points is not defined, although it is assumed that each line looks just like the 'number line', the set of real numbers. Intuitively, this means that we can place the ruler (number line) down on any line and set up a 1-1 correspondence from the points on the line to the real numbers. That is what the Ruler Axiom states.

RA (Ruler Axiom) There is a one-to-one correspondence from the points on a line to the real numbers so that the distance from A to B on the line is the absolute value of the difference of the numbers a and b corresponding to the points.

>

Notation . The distance from point A to point B is denoted by AB.

Definition . If the ruler has been placed on a line, then the number x corresponding to the point X on the line is called the ' coordinate ' of the point.

Exercise 2. Use the ruler axiom to show that distance has these properties

(i) AB = BA.

(ii) and AB= 0 if and only if A = B.

Solution. Lay the ruler down on line(AB) and let a and b be the coordinates of A and B respectively.

(i) Now by the notation, AB = and BA = . But by properties of absolute value, , so AB = BA.

(ii) = AB by properties of absolute value. The second part is true because the correspondence set up by the ruler is 1-1: different points have different coordinates.

Definition. If A, B, and C are distinct points on a line, then B is between A and C if AB + BC = AC.

T2 If B is between A and C, and C is between B and D, then B is between A and D and C is between A and D.

>

Proof . We will show that B is between A and D. The proof that C is between A and D is similar.

First to see that A, B, and D lie on a line, we know that A, B, and C lie on line(BC) since B is between A and C. Also B, C, and D lie on line(BC) since C is between B and D. Hence A, B, and D lie on line(BC).

Next, to see that AB+BD = AD, lay the ruler down on line(AB) and let a, b, c and d be the coordinates of A, B, C, and D respectively. We can assume that a < b, for otherwise just turn the ruler over lengthwise and lay it back down. Hence AB = . Now B is between A and C, so AB+BC = AC, and so by the ruler axiom,

(1)

By the order axioms for numbers, either c < a < b, or a < c < b, or a < b < c. But if c < a, then (1) becomes , which says that b = a, a contradiction since A, B and C are distinct and different points have different coordinates by RA. Likewise if a < c < b, (1) becomes , which says that b = c, also a contradiction. Hence we have a < b < c. In the same way, from C between B and D and b < c, we get that b < c < d. Hence a < b < d and so

or AB + BD = AD. This proves that B is between A and D. qed .

Exercise 3 . Show that given any three distinct points on a line, one of them is between the other two. Use the ruler axiom.

Solution . Let l be a line and let A, B, and C be distinct points on l. Lay the ruler down on l and let a, b, and c be the coordinates of A, B, and C respectively. The trichotomy axiom for real numbers tells us that a, b, and c are arranged in one of 6 possible ways: a < b < c or c < b < a or b < a < c or c < a < b or a < c < b or b < c < a. We claim that in each case one of A, B, and C is between the other two. The argument is similar for each case: let's do the 4th case c < a < b. Here we see that CA = , AB = and CB = . Hence CA + AB = = CB, and so A is between C and B in this case. qed

Exercise 4 . Let A = [3,4], , and C = [x,3]. Find x so that A, B, and C lie on a line. Which is between the other two?

Solution : Since the 2nd coordinate of A lies between the 2nd coordinates of C and B, A should lie between C and B. We can write an equation for the line thru A and B 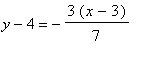. Now if C is going to satisfy this equation, 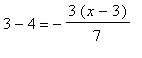, or x = . Checking that CA + AB = CB:

CA = 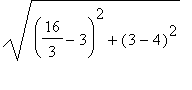= 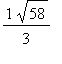, AB = 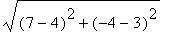= , and CB = 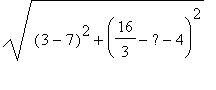= 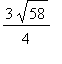, so indeed C is between A and B.

> A:=[3,4]: B:= [-4,7]: C:=[x,3]:

> eqn := y - A[2] = (B[2]-A[2])/(B[1]-A[1])*(x - A[1]);

> solx := solve(subs(y=3,eqn),{x});

> dist := (p,q) -> sqrt((p[1]-q[1])^2+(p[2]-q[2])^2);

> dist([16/3,3],A),dist(A,B) , dist([16/3,3],B) ;

>

Definition. Let A and B be distinct points. The ray starting at A and passing through B, denoted ray(AB), is the set of all points X such that X = A, or X is between A and B, or X = B, or B is between A and X.

T3 . If A and B are distinct points, then the line(AB) is the union of the ray(AB) with the ray (BA).

>

Proof . We will show that T3 follows from Exercise 3 above. Let X be a point on the line(AB). Then by the exercise, A is between X and B (in which case X is on the ray(BA)), X is between A and B (in which case X is on both rays), or B is between A and X (in which case X is on the ray(AB)). So the line(AB) is a subset of the union of the rays. On the other hand, let X be in the union of the rays. Then it is in one of them, and in either case it is collinear with A and B, so the union of the rays is a subset of the line. So

line(AB) = ray(AB) union ray(BA). qed .

Definition . Let A and B be distinct points. The segment seg(AB) is defined as the set of all points X such that X = A or X = B or X is between A and B.

Definition . A set S of points in the plane is convex if given any two points A and B in S, the segment seg(AB) is a subset of S.

Exercise . Let A and B be points. Then the line(AB) is convex. Also the ray(AB) is convex.

Solution: To show line(AB) is convex, let P and Q be points on the line. Then seg(PQ) consists of P, Q and all points on the line(PQ) which are between P and Q. In particular, points on the segment seg(PQ) lie on the line(PQ). But line(PQ) = line(AB) by I2 (P and Q lie on line(AB)). qed .

Exercise . Let S and T be convex sets. Show that intersection of S and T is convex.

Solution: Let A and B be points in the intersection of S and T. We want to show that the seg(AB) is a subset of the intersection of S and T. Let X be a point in seg(AB). Then X is in S since S is convex. X is also in T since T is convex. So X is in the intersection of S and T. Hence seg(AB) is a subset of S intersect T. qed.

PS Each line separates the plane into two disjoint convex sets (called sides of the line) such that any segment which contains a point from each side contains a point from the line.

>

Notation . If l is a line and H and K are the two sides of the line in the plane, then if C is a point in H, then H is called the C-side of l

Definition . A set of points is said to be collinear if ........

Definition . Let A, B, and C be noncolliner points. The triangle ABC is the union of the segments seg(AB), seg(BC) and seg(CA). A, B, and C are called the ........... of the triangle and the segments which make up the triangle are called the ............ of the triangle.

T4 . If a line l meets one side of a triangle, then it meets another side of the triangle.

Hint: Use the plane separation axiom (PS), the ruler axiom (RA), and the second incidence axiom (I2).

>

next