![[Maple OLE 2.0 Object]](images/theory41.gif)
Theory of similar triangles
T26 If three or more parallel lines intercept congruent segments on one transversal, they intercept congruent segments on every transversal.
![[Maple OLE 2.0 Object]](images/theory41.gif)
Given : l, m, and n are parallel with transversals t and s. AB = BC
To show: A'B' = B'C'
Idea of Proof: Use RA to mark D between B and B' so that AA' = DB' and E between C and C' so that BB' = EC'.
Use SAS to show triangle ADA' is congruent with triangle B'A'D. Then conclude AD = A'B' and angle(ADA') is congruent with angle(B'A'D) (why?) Then conclude line(AD) is parallel with line s (why?). In a similar way, argue that BE = B'C' and line(BE) is parallel with s. Now know line(AD) is parallel with line(BE). (why?). Now use a couple of theorems and ASA to conclude that triangle(ABD) is congruent with triangle(BCE). So AD = BE (why?). So A'B' = B'C' (why?) qed
T27 If a segment joins the midpoints of two sides of a triangle, then it is parallel to the third side and has half the length of the third side.
Given : triangle ABC and M and N midpoints of AC and BC respectively.
Show MN is parallel with AB and MN = 1/2 AB.
Idea of Proof. Draw the line l through M parallel to AB and the line through C parallel to AB. By T26, l must bisect BC at N, so MN = l is parallel with AB. Now draw the line t through M parallel with BC and the line through A parallel with BC. Again by T26, t must bisect AB at a point R. By ASA (T8.5), triangle ARM is congruent with triangle MNC and so MN = AR = 1/2 of AB. qed.
Definition
. Two triangles ABC and DEF are similar under the correspondence A to D, B to E, and C to F if the corresponding sides are proportional and the corresponding angles are congruent, that is,
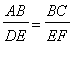 =
=
![]() , and m(angle(A)) = m(angle(D)), m(angle(B)) = m(angle(E)) and m(angle(C)) = m(angle(F))..
, and m(angle(A)) = m(angle(D)), m(angle(B)) = m(angle(E)) and m(angle(C)) = m(angle(F))..
T28 If the three angles of one triangle are congruent to the three angles of another triangle, then the triangles are similar.
Given: triangle(ABC) and triangle(DEF) with m(angle(A)) = m(angle(D)), m(angle(B)) = m(angle(E)), and m(angle(C))= m(angle(F)).
To show:
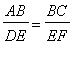 and
and
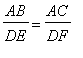
Proof : If AB = DE, then the triangles are congruent and all three ratios are 1. So assume DE > AB.
The proof is by contradiction Assume the second equality fails, say
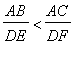 (the argument will be similar if the first fails).
(the argument will be similar if the first fails).
Construct points B' on ray(AB) and C' on ray(AC) so that AB' = DE and AC' = DF. Then triangle(AB'C') is congruent with triangle(DEF), and it will suffice to show
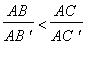 leads to a contradiction. First note that line(BC) is parallel with line(B'C') because angle(ABC) is congruent with angle(AB'C') (why?). Now choose a rational number
leads to a contradiction. First note that line(BC) is parallel with line(B'C') because angle(ABC) is congruent with angle(AB'C') (why?). Now choose a rational number
![]() between
between
![]() and
and
![]() . Cross multiply and get m
. Cross multiply and get m
![]() AB <
AB <
![]() and m
and m
![]() AC >
AC >
![]() . Choose m points
. Choose m points
![]() , ... ,
, ... ,
![]() , ...,
, ...,
![]() on ray(AB) with
on ray(AB) with
![]()
![]() for each i = 1 to
for each i = 1 to
![]() . Construct points
. Construct points
![]() on ray AC so that
on ray AC so that
![]() is parallel with B'C'. Now by T26, the segments
is parallel with B'C'. Now by T26, the segments
![]() are congruent with the segment
are congruent with the segment
![]() for each i. Now
for each i. Now
![]() +
+
![]() + ...
+ ...
![]()
![]() = m (
= m (
![]() AB) <
AB) <
![]() , so
, so
![]() is between A and B'. Also m (
is between A and B'. Also m (
![]() AC) >
AC) >
![]() and so (by a similar argument) C' is between A and
and so (by a similar argument) C' is between A and
![]() . From this we see that
. From this we see that
![]() and
and
![]() are on opposite sides of B'C' and hence the line segments intersect by PS. But they are parallel and we have a contradiction.
qed.
are on opposite sides of B'C' and hence the line segments intersect by PS. But they are parallel and we have a contradiction.
qed.
T29 If two angles of one triangle are congruent to two angles of another, then the triangles are similar.
Hint. Follows quickly from T19 and T28
T30 A line parallel to one side of a triangle that intersects the other two sides in distinct point divides these two sides into proportional segments.
Hint. A special case of T28.
T31 A line that intersects two sides of a triangle in distinct points and divides these two sides into proportional segments is parallel to the third side.
Given : triangle(ABC) with D between A and B and E between A and C so that AD/AB = AE/AC.
To show: DE is parallel with BC.
Hint on proof. Construct point E' on AC so that DE' is parallel with BC. Then use T30 to argue that AD/AB = AE'/AC. Then use RA to argue that E = E'.
T32 If two pairs of corresponding sides of two triangles are proportional and their included angles are congruent, then the two triangles are similar.
Note T30 is the converse of T31. The diagram looks like the diagram for T31, except you can draw MN parallel to BC because that is given.
>
>
T33 If the corresponding sides of two triangles are proportional, then the two triangles are similar.