PALM

Description

PALM implements the Padé Approximate Linearization algorithm: A structure respecting algorithm for solving QEP with low-rank damping

\[ (\lambda^2 M + \lambda C + K) x = 0, \qquad C = EF^{T}, \]

where \(M\), \(C\) and \(K\) are \(n \times n\) matrices, referred to as mass, damping and stiffness matrices. The damping matrix \(C\) is of rank \(\ell \ll n\), which admits the rank-revealing decomposition above with \(E\) and \(F\) to be \(n\times \ell\) full column rank matrices.

The advantage of PALM is that it converts the QEP to a linear eigenvalue problem of dimension \(n_{\rm L} = n+ \ell m\) with \(m\) being the Padé approximation order

\[ \left(\left[\begin{array}{cc} {K}_\sigma +\sigma d C & {E}_{\sigma_1} \\ {F}_{\sigma_2}^{\rm T} & I_{\ell m}\end{array}\right] - \mu \left[\begin{array}{cc} {M}_\sigma & 0 \\ 0 & I_\ell \otimes D_m\end{array}\right]\right) x_{\rm L} = 0, \]

which is significantly smaller than the standard linearization of size \(2n\). (See Ref. [1] for details.)

PALM finds application in solving QEPs arising from analysis of structural dynamics, and acoustic analysis. It runs 33 – 47% faster than the direct linearization (DLIN) approach for solving modest size QEPs.

Contents

MATLAB codes and data

• Main files: pal.m  —  PAL algorithm

• Auxiliary files: Data and demo files for the numerical examples in Ref. [1].

• Download link palm.tar.gz (updated on April 22, 2016).

C++ routines

• A detailed description of the package is here.

• Download link palm++.tar.gz (updated on April 22, 2016).

• Third–party packages  —  those softwares are required, but not delivered with palm++, please download using the link list below.

  • ARPACK++: sparse eigen solver, available at http://www.ime.unicamp.br/~chico/arpack++/

  • SuperLU: sparse LU decomposition, available at http://crd-legacy.lbl.gov/~xiaoye/SuperLU/

    (compatible Version 4.3)

  • LAPACK: linear algebraic library, available at http://www.netlib.org/lapack, also available in MKL library.

Examples

See Ref. [1] for details.

Distribution of eigenvalues

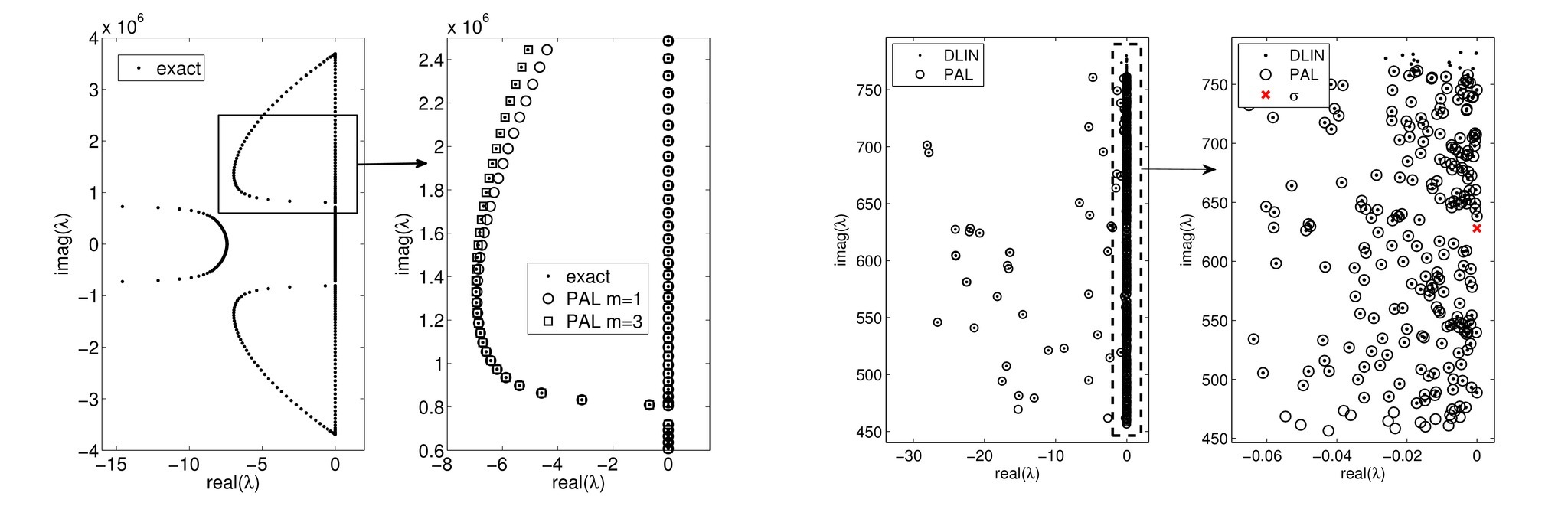Left: damped_beam problem. Right: QEP from car body design.

Timing statistics

Left: damped_beam, n=20K. Middle: acoustic_wave_2d, n= 0.2M. Right: car, n=0.7M.

References

1. A Padé approximate linearization algorithm for solving the quadratic eigenvalue problem with low-rank damping
   by Ding Lu, Xin Huang, Zhaojun Bai, and Yangfeng Su
   Int. J. Numer. Methods Eng., 2015. 103(11): 840–858. (paper)

Contact

Email: Ding.Lu@uky.edu
Homepage: http://www.ms.uky.edu/~dlu245/