TOAR

Description

TOAR is a memory efficient, and numerically reliable algorithm to compute the compact Arnoldi decomposition:

\[ \left[\begin{array}{cc} A & B \\ I & 0 \end{array} \right] \left[\begin{array}{c} Q_kR_{k,1}\\ Q_kR_{k,2} \end{array}\right] = \left[\begin{array}{c} Q_{k+1}R_{k+1,1}\\ Q_{k+1}R_{k+1,2} \end{array}\right] \underline H_{k+1}. \]

It is also a stabilized version of the SOAR procedure to compute the orthonormal basis \(Q_k\) of the second order Krylov subspace

\[ \mathcal{G}_k( A, B; r_{-1}, r_0)\equiv \mbox{span}\{ r_{-1}, r_0, r_1, \dots, r_{k-1}\} \quad\mbox{with}\quad r_ j= A r_{ j-1}+ B r_{ j-2}\quad \mbox{for}\quad j \ge 1. \]

TOAR finds applications in nonlinear eigenvalue computation, and model order reduction. It demonstrates superior performance over the SOAR procedure.

Contents

MATLAB codes and data

• Main files

  • TOAR.m: TOAR procedure

  • SOAR.m: SOAR procedure

• Auxiliary files

  • Data and demo files for the numerical examples in Ref. [1].

• Download link toar.tar.gz (updated on July 1st, 2015).

Examples

See Ref. [1] for details.

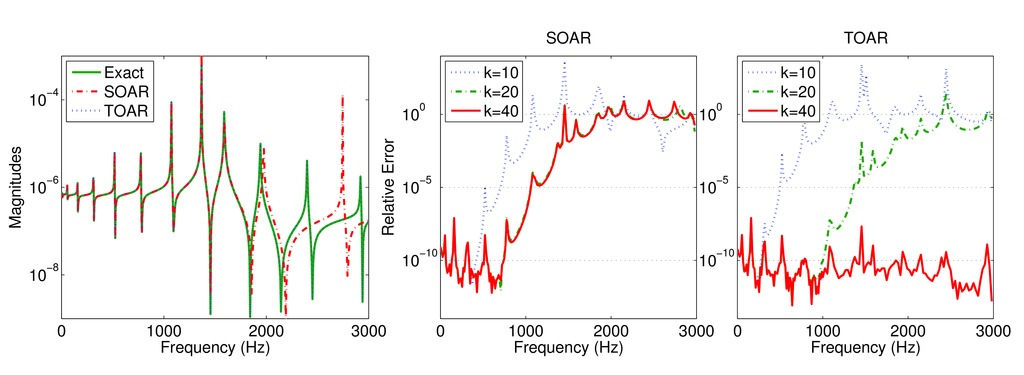References

1. Stability Analysis of the two-level orthogonal Arnoldi procedure
   by Ding Lu, Yangfeng Su and Zhaojun Bai
   SIAM J. Matrix Anal. Appl., 2016. 37(1): 195–214. (paper)

2. SOAR: A second-order Arnoldi method for the solution of the quadratic eigenvalue problem
   by Zhaojun Bai and Yangfeng Su
   SIAM J. Matrix Anal. Appl., 2005. 26(3): 640-659.

Contact

Email: Ding.Lu@uky.edu
Homepage: http://www.ms.uky.edu/~dlu245/