Long Division

Long division is a collapsed version of the Euclidean Division algorithm. First, let’s remind ourselves what the Euclidean Algorithm is:

Euclidean Division Algorithm: If m and n are integers and if n > 0, then there are unique integers q and r such that m = nq + r and .

Another way to write this is to say that with .

Let’s see how you use this to find the decimal representation of any rational number. I will illustrate the process by finding the decimal representation of .

This first application gives us 7, the integer part of this decimal. Each succeeding application uses 10 times the remainder from the previous step. Here are the first 6 lines, which yield a quotient of 7.238095 and a remainder of .

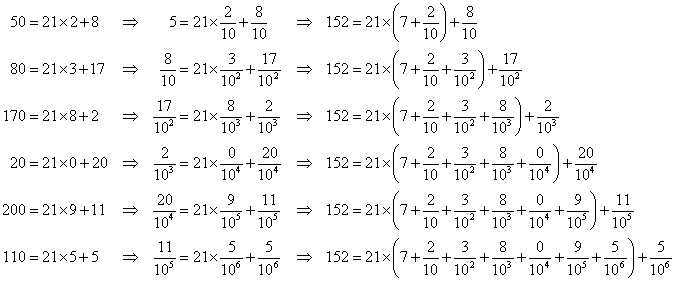
There are only 20 possible non-zero remainders when dividing by 21 so the cycle of the quotients that begins 238095… must repeat after at most 20 steps. In fact, since , the cycle repeats after 6 steps.

Now compare each line with the steps of the calculation from Long Division below. The final remainder 5 is equal to a remainder six steps earlier, so the cycle of quotients, 238095, will be repeated if the long division is continued.