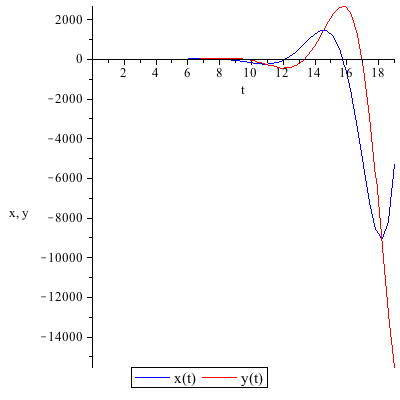
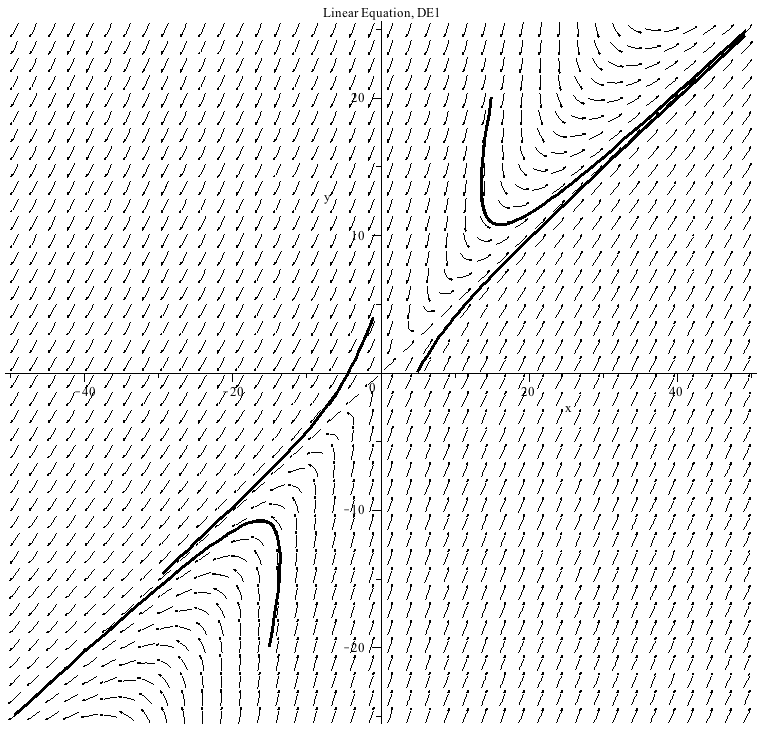
| > |
 |
This system of differential equations (DE1) has two eigenvalues of opposite sign (λ=1 and λ=−2). The point (0,0) is unstable and called a saddle point.
| > |
 |
 |
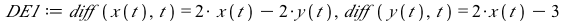
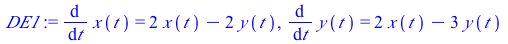(1) |
| > |
 |
 |
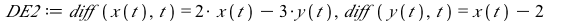
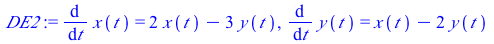(2) |
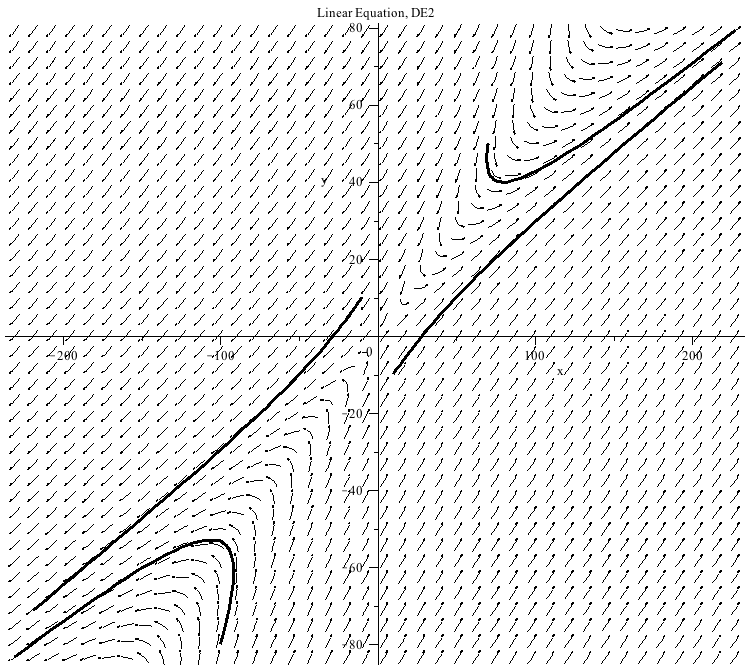
This system of differential equations (DE2) has two eigenvalues of opposite sign (λ=1 and λ=−1). The point (0,0) is unstable and called a saddle point.
| > |
 |
 |
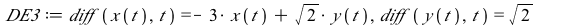
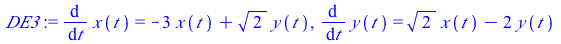(3) |
This system of differential equations (DE3) has two negative eigenvalues (λ=−1 and λ=−4). The point (0,0) is called a sink or a stable node.
| > |
 |
 |
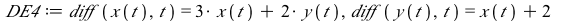
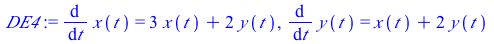(4) |
This system of differential equations (DE4) has two positive eigenvalues (λ=1 and λ=4). The point (0,0) is called a source or an unstable node.
| > |
 |
 |
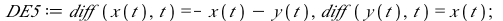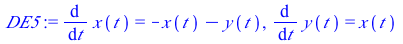(5) |
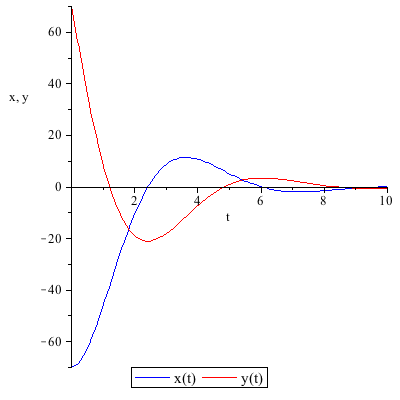
This system of differential equations (DE5) has two complex conjugate eigenvalues (λ=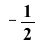
±
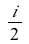
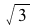) with a negative real part. The point (0,0) is called a stable spiral.
| > |
 |
| > |
 |
 |
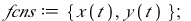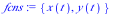(6) |
| > |
 |
 |
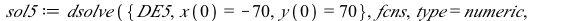
(7) |
| > |
![odeplot(sol5, [[t, x(t)], [t, y(t)]], 0 .. 10, color = [](images/worksheet_lin_diff_eq_52.gif)
![odeplot(sol5, [[t, x(t)], [t, y(t)]], 0 .. 10, color = [](images/worksheet_lin_diff_eq_53.gif) |
| > |
 |
 |
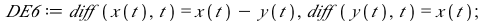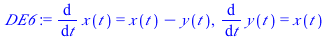(8) |
This system of differential equations (DE6) has two complex conjugate eigenvalues (λ=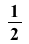
±
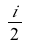
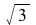) with a positive real part. The point (0,0) is called an unstable spiral.
| > |
 |
| > |
 |
 |
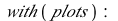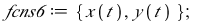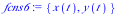(9) |
| > |
 |
 |
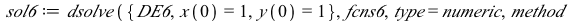
(10) |
| > |
![odeplot(sol6, [[t, x(t)], [t, y(t)]], 0 .. 19, color = [](images/worksheet_lin_diff_eq_71.gif)
![odeplot(sol6, [[t, x(t)], [t, y(t)]], 0 .. 19, color = [](images/worksheet_lin_diff_eq_72.gif) |
![DEplot({DE1}, [x(t), y(t)], t = 0 .. 2, [[x(0) = -1, y(0) = 4], [x(0) = 5, y(0) = 0], [x(0) = 15, y(0) = 20], [x(0) = -15, y(0) = -20]], numsteps = 76, title =](images/worksheet_lin_diff_eq_5.gif){kind=small}
![DEplot({DE1}, [x(t), y(t)], t = 0 .. 2, [[x(0) = -1, y(0) = 4], [x(0) = 5, y(0) = 0], [x(0) = 15, y(0) = 20], [x(0) = -15, y(0) = -20]], numsteps = 76, title =](images/worksheet_lin_diff_eq_6.gif){kind=small}
![DEplot({DE1}, [x(t), y(t)], t = 0 .. 2, [[x(0) = -1, y(0) = 4], [x(0) = 5, y(0) = 0], [x(0) = 15, y(0) = 20], [x(0) = -15, y(0) = -20]], numsteps = 76, title =](images/worksheet_lin_diff_eq_7.gif){kind=small}
![DEplot({DE1}, [x(t), y(t)], t = 0 .. 2, [[x(0) = -1, y(0) = 4], [x(0) = 5, y(0) = 0], [x(0) = 15, y(0) = 20], [x(0) = -15, y(0) = -20]], numsteps = 76, title =](images/worksheet_lin_diff_eq_8.gif){kind=small}
![DEplot({DE2}, [x(t), y(t)], t = 0 .. 2, [[x(0) = 10, y(0) = -10], [x(0) = 70, y(0) = 50], [x(0) = -10, y(0) = 10], [x(0) = -100, y(0) = -80]], numsteps = 76, title =](images/worksheet_lin_diff_eq_13.gif){kind=small}
![DEplot({DE2}, [x(t), y(t)], t = 0 .. 2, [[x(0) = 10, y(0) = -10], [x(0) = 70, y(0) = 50], [x(0) = -10, y(0) = 10], [x(0) = -100, y(0) = -80]], numsteps = 76, title =](images/worksheet_lin_diff_eq_14.gif){kind=small}
![DEplot({DE2}, [x(t), y(t)], t = 0 .. 2, [[x(0) = 10, y(0) = -10], [x(0) = 70, y(0) = 50], [x(0) = -10, y(0) = 10], [x(0) = -100, y(0) = -80]], numsteps = 76, title =](images/worksheet_lin_diff_eq_15.gif){kind=small}
![DEplot({DE2}, [x(t), y(t)], t = 0 .. 2, [[x(0) = 10, y(0) = -10], [x(0) = 70, y(0) = 50], [x(0) = -10, y(0) = 10], [x(0) = -100, y(0) = -80]], numsteps = 76, title =](images/worksheet_lin_diff_eq_16.gif){kind=small}
![DEplot({DE3}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -40, y(0) = 70], [x(0) = -10, y(0) = -80], [x(0) = 60, y(0) = 40], [x(0) = 1, y(0) = 80], [x(0) = -40, y(0) = -1], [x(0) = 5, y(0) = -80]], numsteps = ...](images/worksheet_lin_diff_eq_21.gif){kind=small}
![DEplot({DE3}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -40, y(0) = 70], [x(0) = -10, y(0) = -80], [x(0) = 60, y(0) = 40], [x(0) = 1, y(0) = 80], [x(0) = -40, y(0) = -1], [x(0) = 5, y(0) = -80]], numsteps = ...](images/worksheet_lin_diff_eq_22.gif){kind=small}
![DEplot({DE3}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -40, y(0) = 70], [x(0) = -10, y(0) = -80], [x(0) = 60, y(0) = 40], [x(0) = 1, y(0) = 80], [x(0) = -40, y(0) = -1], [x(0) = 5, y(0) = -80]], numsteps = ...](images/worksheet_lin_diff_eq_23.gif){kind=small}
![DEplot({DE3}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -40, y(0) = 70], [x(0) = -10, y(0) = -80], [x(0) = 60, y(0) = 40], [x(0) = 1, y(0) = 80], [x(0) = -40, y(0) = -1], [x(0) = 5, y(0) = -80]], numsteps = ...](images/worksheet_lin_diff_eq_24.gif){kind=small}
![DEplot({DE3}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -40, y(0) = 70], [x(0) = -10, y(0) = -80], [x(0) = 60, y(0) = 40], [x(0) = 1, y(0) = 80], [x(0) = -40, y(0) = -1], [x(0) = 5, y(0) = -80]], numsteps = ...](images/worksheet_lin_diff_eq_25.gif){kind=small}
![DEplot({DE4}, [x(t), y(t)], t = 0 .. .75, [[x(0) = -40, y(0) = 50], [x(0) = 1, y(0) = 20], [x(0) = -1, y(0) = -10], [x(0) = -20, y(0) = 8], [x(0) = 60, y(0) = -50], [x(0) = -100, y(0) = 75], [x(0) = 1...](images/worksheet_lin_diff_eq_30.gif){kind=small}
![DEplot({DE4}, [x(t), y(t)], t = 0 .. .75, [[x(0) = -40, y(0) = 50], [x(0) = 1, y(0) = 20], [x(0) = -1, y(0) = -10], [x(0) = -20, y(0) = 8], [x(0) = 60, y(0) = -50], [x(0) = -100, y(0) = 75], [x(0) = 1...](images/worksheet_lin_diff_eq_31.gif){kind=small}
![DEplot({DE4}, [x(t), y(t)], t = 0 .. .75, [[x(0) = -40, y(0) = 50], [x(0) = 1, y(0) = 20], [x(0) = -1, y(0) = -10], [x(0) = -20, y(0) = 8], [x(0) = 60, y(0) = -50], [x(0) = -100, y(0) = 75], [x(0) = 1...](images/worksheet_lin_diff_eq_32.gif){kind=small}
![DEplot({DE4}, [x(t), y(t)], t = 0 .. .75, [[x(0) = -40, y(0) = 50], [x(0) = 1, y(0) = 20], [x(0) = -1, y(0) = -10], [x(0) = -20, y(0) = 8], [x(0) = 60, y(0) = -50], [x(0) = -100, y(0) = 75], [x(0) = 1...](images/worksheet_lin_diff_eq_33.gif){kind=small}
![DEplot({DE4}, [x(t), y(t)], t = 0 .. .75, [[x(0) = -40, y(0) = 50], [x(0) = 1, y(0) = 20], [x(0) = -1, y(0) = -10], [x(0) = -20, y(0) = 8], [x(0) = 60, y(0) = -50], [x(0) = -100, y(0) = 75], [x(0) = 1...](images/worksheet_lin_diff_eq_34.gif){kind=small}
![DEplot({DE5}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -70, y(0) = 70], [x(0) = -80, y(0) = -80], [x(0) = 60, y(0) = 40]], numsteps = 76, title =](images/worksheet_lin_diff_eq_41.gif){kind=small}
![DEplot({DE5}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -70, y(0) = 70], [x(0) = -80, y(0) = -80], [x(0) = 60, y(0) = 40]], numsteps = 76, title =](images/worksheet_lin_diff_eq_42.gif){kind=small}
![DEplot({DE5}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -70, y(0) = 70], [x(0) = -80, y(0) = -80], [x(0) = 60, y(0) = 40]], numsteps = 76, title =](images/worksheet_lin_diff_eq_43.gif){kind=small}
![DEplot({DE5}, [x(t), y(t)], t = 0 .. 7, [[x(0) = -70, y(0) = 70], [x(0) = -80, y(0) = -80], [x(0) = 60, y(0) = 40]], numsteps = 76, title =](images/worksheet_lin_diff_eq_44.gif){kind=small}
![DEplot({DE6}, [x(t), y(t)], t = 0 .. 3, [[x(0) = 70, y(0) = 50], [x(0) = -100, y(0) = -80], [x(0) = 180, y(0) = 10]], numsteps = 76, title =](images/worksheet_lin_diff_eq_60.gif){kind=small}
![DEplot({DE6}, [x(t), y(t)], t = 0 .. 3, [[x(0) = 70, y(0) = 50], [x(0) = -100, y(0) = -80], [x(0) = 180, y(0) = 10]], numsteps = 76, title =](images/worksheet_lin_diff_eq_61.gif){kind=small}
![DEplot({DE6}, [x(t), y(t)], t = 0 .. 3, [[x(0) = 70, y(0) = 50], [x(0) = -100, y(0) = -80], [x(0) = 180, y(0) = 10]], numsteps = 76, title =](images/worksheet_lin_diff_eq_62.gif){kind=small}
![DEplot({DE6}, [x(t), y(t)], t = 0 .. 3, [[x(0) = 70, y(0) = 50], [x(0) = -100, y(0) = -80], [x(0) = 180, y(0) = 10]], numsteps = 76, title =](images/worksheet_lin_diff_eq_63.gif){kind=small}
