S程序设计

对于复杂一些的计算问题我们应该编写成函数。这样做的好处是编写一次可以重复使用，并且可以很容易地修改，另外的好处是函数内的变量名是局部的，运行函数不会使函数内的局部变量被保存到当前的工作空间，可以避免在交互状态下直接赋值定义很多变量使得工作空间杂乱无章。

工作空间管理

前面我们已经提到，S在运行时保持一个变量搜索路径表，要读取某变量时依次在此路径表中查找，返回找到的第一个；给变量赋值时在搜索路径的第一个位置赋值。但是，在函数内部，搜索路径表第一个位置是局部变量名空间，所以变量赋值是局部赋值，被赋值的变量只在函数运行期间有效。

用ls()函数可以查看当前工作空间保存的变量和函数，用rm()函数可以剔除不想要的对象。如：

> ls()
 [1] "A"     "Ai"    "b"     "cl"    "cl.f"  "fit1"  "g1"    "marks" "ns"   
[10] "p1"    "rec"   "tmp.x" "x"     "x1"    "x2"    "x3"    "y"    
> rm(x, x1, x2, x3)
> ls()
 [1] "A"     "Ai"    "b"     "cl"    "cl.f"  "fit1"  "g1"    "marks" "ns"   
[10] "p1"    "rec"   "tmp.x" "y"

ls()可以指定一个pattern参数，此参数定义一个匹配模式，只返回符合模式的对象名。模式格式是UNIX中grep的格式。比如，ls(pattern="tmp[.]")可以返回所有以“tmp.” 开头的对象名。

rm()可以指定一个名为list的参数给出要删除的对象名，所以rm(list=ls(pattern="tmp[.]")) 可以删除所有以“tmp.”开头的对象名。

函数定义

S中函数定义的一般格式为“函数名 <- function(参数表) 表达式”。定义函数可以在命令行进行，例如：

> hello <- function(){
+   cat("Hello, world\n")
+   cat("\n")
+ }
> hello
function () 
{
	    cat("Hello, world\n")
	    cat("\n")
}
> hello()
Hello, world

函数体为一个复合表达式，各表达式的之间用换行或分号分开。不带括号调用函数显示函数定义，而不是调用函数。

在命令行输入函数程序很不方便修改，所以我们一般是打开一个其他的编辑程序（如Windows 的记事本），输入以上函数定义，保存文件，比如保存到了C:\R\hello.s，我们就可以用

> source("c:\\R\\hello.s")

运行文件中的程序。实际上，用source()运行的程序不限于函数定义，任何S程序都可以用这种方式编好再运行，效果与在命令行直接输入是一样的。

对于一个已有定义的函数，可以用fix()函数来修改，如：

> fix(hello)

将打开一个编辑窗口显示函数的定义，修改后关闭窗口函数就被修改了。fix()调用的编辑程序缺省为记事本，可以用“options(editor="编辑程序名")”来指定自己喜欢的编辑程序。

函数可以带参数，可以返回值，例如：

larger <- function(x, y){
  y.is.bigger <- (y>x);
  x[y.is.bigger] <- y[y.is.bigger]
  x
}

这个函数输入两个向量（相同长度）x和y，然后把x中比y对应元素小的元素替换为y中对应元素，返回y的值。S返回值为函数体的最后一个表达式的值，不需要使用return()函数。不过，也可以使用“return( 对象)”函数从函数体返回调用者。

参数（自变量）

函数可以带虚参数（形式自变量）。S函数调用方式很灵活，例如，如下函数：

fsub <- function(x, y) x-y

有两个虚参数x和y，我们用它计算100－45，可以调用fsub(100,45)，或fsub(x=100,y=45) ，或fsub(y=45, x=100)，或fsub(y=45, 100)。即调用时实参与虚参可以按次序结合，也可以直接指定虚参名结合。实参先与指定了名字的虚参结合，没有指定名字的按次序与剩下的虚参结合。

函数在调用时可以不给出所有的实参，这需要在定义时为虚参指定缺省值。例如上面的函数改为：

fsub <- function(x, y=0) x-y

则调用时除了可以用以上的方式调用外还可以用fsub(100)，fsub(x=100)等方式调用，只给出没有缺省值的实参。

即使没有给虚参指定缺省值也可以在调用时省略某个虚参，然后函数体内可以用missing() 函数判断此虚参是否有对应实参，如：

trans <- function(x, scale){
  if(!missing(scale)) x <- scale*x
  …………
}

此函数当给了scale的值时对自变量x乘以此值，否则保持原值。这种用法在其它语言中是极其少见的，S可以实现这一点是因为S的函数调用在用到参数的值时才去计算这个参数的值（称为“懒惰求值”），所以可以在调用时缺少某些参数而不被拒绝。

S函数还可以有一个特殊的“...”虚参，表示所有不能匹配的实参，调用时如果有需要与其它虚参结合的实参必须用“虚参名＝”的格式引入。例如：

> f <- function(...){
+   for(x in list(...))
+   cat(min(x), '\n')
+ }
> f(c(5,1,2), c(9, 4, 7))
1 
4

作用域

	函数的虚参完全是按值传递的，改变虚参的值不能改变对应实参的值。例如：
> x <- list(1, "abc")
> x
[[1]]
[1] 1
　
[[2]]
[1] "abc"
　
> f <- function(x) x[[2]] <- "!!"
> f(x)
> x
[[1]]
[1] 1
　
[[2]]
[1] "abc"

函数体内的变量也是局部的，对函数体内的变量赋值当函数结束运行后变量值就删除了，不影响原来同名变量的值。例如：

> x <- 2
> f <- function(){
+   print(x)
+   x <- 20
+ }
> f()
[1] 2
> x
[1] 2

这个例子中原来有一个变量x值为2，函数中为变量x赋值20，但函数运行完后原来的x值并未变化。但是也要注意，函数中的显示函数调用时局部变量x还没有赋值，显示的是全局变量x 的值。这是S编程比较容易出问题的地方：你用到了一个局部变量的值，你没有意识到这个局部变量还没有赋值，而程序却没有出错，因为这个变量已有全局定义。

程序调试

S-PLUS和R目前还不象其它主流程序设计语言那样具有单步跟踪、设置断点、观察表达式等强劲的调试功能。调试复杂的S程序，可以用一些通用的程序调试方法，另外S也提供了一些调试用函数。

对任何程序语言，最基本的调试手段当然是在需要的地方显示变量的值。可以用print() 或cat()显示。例如，我们为了调试前面定义的larger()函数，可以显示两个自变量的值及中间变量的值：

larger <- function(x, y){
  cat('x = ', x, '\n')
  cat('y = ', y, '\n')
  y.is.bigger <- (y>x);
  cat('y.is.bigger = ', y.is.bigger, '\n')
  x[y.is.bigger] <- y[y.is.bigger]
  x
}

S提供了一个browser()函数，当调用时程序暂停，用户可以查看变量或表达式的值，还可以修改变量。例如：

larger <- function(x, y){
  y.is.bigger <- (y>x);
  browser()
  x[y.is.bigger] <- y[y.is.bigger]
  x
}

我们运行此程序：

> larger(c(1,5), c(2, 4, 9))
Warning in y > x : longer object length
        is not a multiple of shorter object length
Called from: larger(c(1, 5), c(2, 4, 9))
Browse[1]> y
[1] 2 4 9
Browse[1]> x
[1] 1 5
Browse[1]> y>x
Warning in y > x : longer object length
        is not a multiple of shorter object length
[1]  TRUE FALSE  TRUE
Browse[1]> c
Error: subscript (3) out of bounds, should be at most 2

退出R的browser()菜单可用c（在S中用return()）。在R的browser()状态下用n命令可以进入单步执行状态，用n或者回车可以继续，用c可以退出。

R提供了一个debug()函数，debug(f)可以打开对函数f()的调试，执行到函数f时自动进入单步执行的browser()菜单。用undebug(f)关闭调试。

程序设计举例

设计S程序是很容易的，在初学时我们只要使用我们从一般程序设计中学来的知识并充分利用S中现成的各种算法及绘图函数就可以了。但是，如果要用S编制计算量较大的程序，或者程序需要发表，就需要注意一些S程序设计的技巧。

用S语言开发算法，最重要的一点是要记住S是一个向量语言，计算应该尽量通过向量、矩阵运算来进行，或者使用S提供的现成的函数，避免使用显式循环。显式循环会大大降低S的运算速度，因为S是解释执行的。

比如，考虑核回归问题。核回归是非参数回归的一种，假设变量 Y与变量 X之间的关系为：

其中函数 f未知。观测到X和Y的一组样本， i=1,..., n后，对 f的一种估计为：

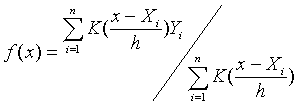
其中 K叫做核函数，一般是一个非负的偶函数，原点处的函数值最大，在两侧迅速趋于零。例如正态密度函数，或所谓双三次函数核：

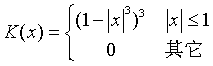
函数density()可以进行核回归估计，这里作为举例我们对这个算法进行编程。先来编制双三次核函数的程序：

kernel.dcube <- function(u){
  y <- numeric(length(u))
  y[abs(u)<1] <- (1 - abs(u[abs(u)<1])^3)^3
  y[abs(u)>=1] <- 0
  y
}

注意上面分段函数不用if语句而是采用逻辑向量作下标的办法，这样定义出的函数允许以向量和数组作自变量。

假设我们要画出核估计曲线，一般我们取一个范围与各范围相同的等间距向量 x然后计算估计出的 f( x)的值。设观测数据自变量保存在向量X中，因变量保存在向量Y中，则按我们一般的程序设计思路，可以写成下面的S程序：

kernel.smooth1 <- function(X, Y, kernel=kernel.dcube, h=1, m=100, plot.it=T){
  x <- seq(min(X), max(X), length=m)
  fx <- numeric(m)
  for(j in 1:m){
    # 计算第j个等间距点的回归函数估计值
    fx[j] <- sum(kernel((x[j]-X)/h)*Y) / sum(kernel((x[j]-X)/h))
  }
  if(plot.it){
    plot(X, Y, type="p")
    lines(x, fx)
  }
  cbind(x=x, fx=fx)
}

注意上面程序中用了sum函数来避免一重对 i的循环。但是，上面的写法中仍有一重对j的循环，使得程序运行较慢。如何改写程序把这个循环也取消呢？办法是把计算看成是矩阵运算。首先，如果x是一个标量，则f(x)可以写成：

其中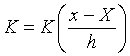是一个与 X长度相等（即长度为 n）的行向量，是一列1。现在，x实际是一个长度为 m的向量，对x的每一个元素可以计算一个长度为 n的行向量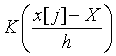，把这些行向量上下合并为一个矩阵 K，则 KY为长度为 m的向量，每一个元素是对应于一个x[j]的分子。合并的矩阵可以用S的outer()函数来计算：

K <- outer(x, X, function(u, v) kernel((u-v)/h))

# outer()的第一个自变量对应于结果矩阵的行，第二个自变量对应于列

分母为了算每一行的和只要对 K右乘，于是结果的估计值向量为：

fx <- (K %*% Y) / (K %*% matrix(1,ncol=1,nrow=length(Y))

这样修改kernel.smooth1可以得到更精简的函数kernel.smooth2。这种方法在R中可以实现，但在Splus中运行却有问题，因为Splus不允许函数内部再定义函数。

核回归中窗宽 h的选择是比较难的，我们写的核回归函数应该允许用户输入 h为一个向量，对向量中每一个窗口计算一条拟合曲线并画在图中，结果作为函数返回值的一列。读者可以作为练习实现这个函数，并模拟X和Y的观测然后画核估计曲线， f( x)用sin(x)。对 h我们可能必须用循环来处理了。