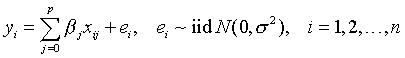
这一节我们简单介绍S的统计模型。S中实现了几乎所有常见的统计模型,而且多种模型可以用一种统一的观点表示和处理。这方面S-PLUS较全面,它实现了许多最新的统计研究成果,R因为是自愿无偿工作所以统计模型部分还相对较欠缺。事实上,许多统计学家的研究出的统计算法都以S-PLUS程序发表,因为S语言是一种特别有利于统计计算编程的语言。
学习这一节需要我们具备线型模型、线型回归、方差分析的基本知识。
很多统计模型可以用一个线型模型来表示:
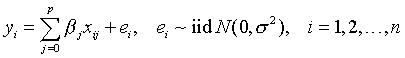
写成矩阵形式为
![]()
其中 ![]() 为因变量,
为因变量, ![]() 为模型矩阵或称设计阵,各列为
为模型矩阵或称设计阵,各列为 ![]() ,
, ![]() ,...,
,..., ![]() 等各自变量,其中
等各自变量,其中 ![]() 常常是一列1,定义一个模型截距项。
常常是一列1,定义一个模型截距项。
在S中模型是一种对象,其表达形式叫做一个公式,我们先举几个例子来看一看。假定y,x,x0,x1,x2,…是数值型变量,X是矩阵,A,B,C,…是因子。
|
y ~ x y ~ 1 + x |
两个式子都表示y对x的简单一元线型回归。第一个式子带有隐含的截距项,而第二个式子把截距项显式地写了出来。 |
|
y ~ -1 + x y ~ x - 1 |
都表示y对x的通过原点的回归,即不带截距项的回归。 |
|
log(y) ~ x1 + x2 |
表示log(y)对x1和x2的二元回归,带有隐含的截距项。 |
|
y ~ poly(x, 2) y ~ 1 + x + I(x^2) |
表示y对x的一元二次多项式回归。第一种形式使用正交多项式,第二种形式直接使用x的各幂次。 |
|
y ~ X + poly(x,2) |
因变量为y的多元回归,模型矩阵包括矩阵X,以及x的二次多项式的各项。 |
|
y ~ A |
一种方式分组的方差分析,指标为y,分组因素为A。 |
|
y ~ A + x |
一种方式分组的协方差分析,指标为y,分组因素为A,带有协变量x。 |
y ~ A*B y ~ A + B + A:B y ~ B %in% A y ~ A/B |
非可加两因素方差分析模型,指标为y,A,B是两个因素。前两个公式表示相同的交叉分类设计,后两个公式表示相同的嵌套分类设计。 |
|
y ~ (A + B + C)^2 y ~ A*B*C - A:B:C |
表示三因素试验,只考虑两两交互作用而不考虑三个因素间的交互作用。两个公式是等价的。 |
y ~ A * x y ~ A / x y ~ A / (1 + x) - 1 |
都表示对因子A的每一水平拟合y对x的线型回归,但三个公式的编码方式不同。最后一种形式对A的每一水平都分别估计截距项和斜率项。 |
|
y ~ A*B + Error(C) |
表示有两个处理因素A和B,误差分层由因素C确定的设计 |
在S中~运算符用来定义模型公式。一般的线型模型的公式形式为
因变量 ~ ![]() 第一项
第一项 ![]() 第二项
第二项 ![]() 第三项
第三项 ![]() …
…
其中因变量可以是向量或矩阵,或者结果为向量或矩阵的表达式。 ![]() 是加号+或者减号-,表示在模型中加入一项或去掉一项,第一项前面如果是加号可以省略。
是加号+或者减号-,表示在模型中加入一项或去掉一项,第一项前面如果是加号可以省略。
公式中的各项可以取为:
每一项定义了要加入模型矩阵或从模型矩阵中删除的若干列。一个1表示一个截距项列,除非显式地删除总是隐含地包括在模型公式中。
“公式运算符”的定义和Glim、Genstat软件中的定义类似,不过那里的“.”运算符这里改成了“:”,因为在S中句点是名字的合法字符。下表列出了各运算符的简要说明。
|
运算符 |
含义 |
|
Y ~ M |
Y作为因变量由 M解释。 |
|
|
加入 |
|
|
加入 |
|
|
|
|
|
与 |
|
|
等于 |
|
|
等于 |
|
M^ n |
M中所有各项以及所有到 n阶为止的交互作用项。 |
|
I( M) |
将 M隔离,使得 M中的运算符按照原来的算术运算符解释而不是按公式运算符解释。表达式 M的结果作为公式的一项。 |
注意在函数调用的括号内的表达式按普通四则运算解释。函数I()可以把一个计算表达式封装起来作为模型的一项使用。
注意S的模型表示只给出了因变量和自变量及自变量间的关系,这样只确定了线型模型的模型矩阵,而模型参数向量是隐含的,并没有的模型公式中体现出来。这种做法适用于线性模型,但不具有普遍性,例如非线性模型就不能这样表示。
拟合普通的线性模型的函数为lm(),其简单的用法为:
> fitted.model <- lm( formula, data= data.frame)
其中data.frame为各变量所在的数据框,formula为模型公式,fitted.model是线性模型拟合结果对象(其class属性为lm)。例如:
> mod1 <- lm(y ~ x1 + x2, data=production)
可以拟合一个y对x1和x2的二元回归(带有隐含的截距项),数据来自数据框production 。拟合的结果存入了对象mod1中。注意不论数据框production是否以用attach()连接入当前运行环境都可被lm()使用。lm()的基本显示十分简练:
> mod1 Call: lm(formula = y ~ x1 + x2, data = production) Coefficients: (Intercept) x1 x2 0.0122033 2.0094758 -0.0005314只显示了调用的公式和参数估计结果。
lm()函数的返回值叫做模型拟合结果对象,本质上是一个具有类属性值lm的列表,有model 、coefficients、residuals等成员。lm()的结果显示十分简单,为了获得更多的拟合信息,可以使用对lm类对象有特殊操作的通用函数,这些函数包括:
add1 coef effects kappa predict residuals alias deviance family labels print summary anova drop1 formula plot proj下表给出了lm类(拟合模型类)常用的通用函数的简单说明。
|
通用函数 |
返回值或效果 |
|
anova(对象1,对象2) |
把一个子模型与原模型比较,生成方差分析表。 |
|
coefficients(对象) |
返回回归系数(矩阵)。可简写为coef(对象)。 |
|
deviance(对象) |
返回残差平方和,如有权重则加权。 |
|
formula(对象) |
返回模型公式。 |
|
plot(对象) |
生成两张图,一张是因变量对拟合值的图形,一张是残差绝对值对拟合值的图形。 |
predict(对象, newdata=数据框) predict.gam(对象, newdata=数据框) |
有了模型拟合结果后对新数据进行预报。指定的新数据必须与建模时用的数据具有相同的变量结构。函数结构为对数据框中每一观测的因变量预报结果(为向量或矩阵)。 predict.gam()与predict()作用相同但适用性更广,可应用于lm、glm和gam的拟合结果。比如,当多项式基函数用了正交多项式时,加入了新数据导致正交多项式基函数改变,用predict.gam() 函数可以避免由此引起的偏差。 |
|
print(对象) |
简单显示模型拟合结果。一般不用print()而直接键入对象名来显示。 |
|
residuals(对象) |
返回模型残差(矩阵),若有权重则适当加权。可简写为resid(对象)。 |
|
summary(对象) |
可显示较详细的模型拟合结果。 |
方差方差分析是研究取离散值的因素对一个数值型指标的影响的经典工具。S进行方差分析的函数是aov(),格式为aov(公式,data=数据框),用法与lm()类似,提取信息的各通用函数仍有效。
我们以前面用过的不同牌子木板磨损比较的数据为例。假设veneer数据框保存了该数据:
> veneer Brand Wear 1 ACME 2.3 2 ACME 2.1 3 ACME 2.4 4 ACME 2.5 5 CHAMP 2.2 6 CHAMP 2.3 7 CHAMP 2.4 8 CHAMP 2.6 9 AJAX 2.2 10 AJAX 2.0 11 AJAX 1.9 12 AJAX 2.1 13 TUFFY 2.4 14 TUFFY 2.7 15 TUFFY 2.6 16 TUFFY 2.7 17 XTRA 2.3 18 XTRA 2.5 19 XTRA 2.3 20 XTRA 2.4首先我们把每个牌子的木板的磨损情况画盒形图并且放在同一页面中,作图如下:
plot(Wear ~ Brand, data=veneer)
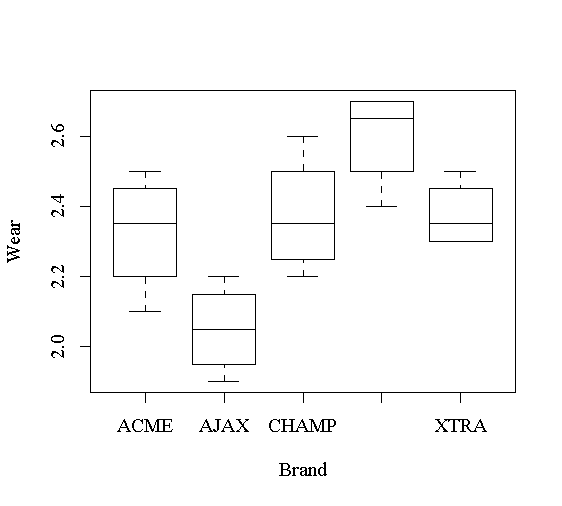
见图11。这种图可以直观地比较一个变量在多个组的分布,或者比较几个类似的变量。从图中可以看出,AJAX牌子较好,TUFFY较差,其它三个牌子差别不明显。
为了检验牌子这个因素对指标磨损量有无显著影响,只要用aov()函数:> aov.veneer <- aov(Wear ~ Brand, data=veneer)
> summary(aov.veneer)
Df Sum Sq Mean Sq F value Pr(>F)
Brand 4 0.61700 0.15425 7.404 0.001683 **
Residuals 15 0.31250 0.02083
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
可见因素是显著的。
下面我们以7.1.2中的那个学生班的情况为例进行一些分析。我们希望了解体重、身高、年龄、性别等变量的基本情况及互相之间的关系。
假设数据放在了文本文件c:\work\class.txt中,没有列标题,各变量上下对齐。我们先把数据读入一个S数据框对象中:
> cl <- read.table("c:/work/class.txt",
+ col.names=c("Name", "Sex", "Age", "Height", "Weight"),
+ row.names="Name")
> cl
Sex Age Height Weight
Alice F 13 56.5 84.0
Becka F 13 65.3 98.0
Gail F 14 64.3 90.0
Karen F 12 56.3 77.0
Kathy F 12 59.8 84.5
Mary F 15 66.5 112.0
Sandy F 11 51.3 50.5
Sharon F 15 62.5 112.5
Tammy F 14 62.8 102.5
Alfred M 14 69.0 112.5
Duke M 14 63.5 102.5
Guido M 15 67.0 133.0
James M 12 57.3 83.0
Jeffrey M 13 62.5 84.0
John M 12 59.0 99.5
Philip M 16 72.0 150.0
Robert M 12 64.8 128.0
Thomas M 11 57.5 85.0
William M 15 66.5 112.0
首先我们先研究各变量的分布情况,看分布是否接近正态,有无明显的异常值,有没有明显的序列相关,等等。
研究连续型变量的分布,可以使用直方图、盒形图、分布密度估计图和正态概率图。研究离散型变量分布只要画其分布频数条形图即可,分布频数用table函数计算。研究序列相关性可以作时间序列图和自相关函数图。因为这些图经常重复使用,我们把它们定义为函数,在同一页面画出:
function(x) {
oldpar <- par(mfrow = c(2, 2),
mar=c(2,2,0.2,0.2),
mgp=c(1.2,0.2,0))
hist(x, main="", xlab="", ylab="")
boxplot(x)
iqd <- summary(x)[5] - summary(x)[2]
plot(density(x,width=2*iqd), xlab = "x",
ylab = "", type = "l", main="")
qqnorm(x, main="", xlab="", ylab="")
qqline(x)
par(oldpar)
invisible()
}
function(x) {
oldpar <- par(mfrow=c(2,1),
mar=c(2,2,1,0.2), mgp=c(1.2, 0.2, 0))
plot.ts(x, main="", xlab="")
acf(x, main="", xlab="")
par(oldpar)
invisible()
}
函数中最后的invisible()表示在命令行调用此函数时不要显示任何返回值。变量iqd 计算的是函数的四分位间距。函数density用来作核密度曲线估计,其width参数为核估计的参数。现在调用这些函数来研究各数值型变量的分布情况。在调用前先把数据框cl连接入当前的搜索路径中以直接使用cl中的变量名:
> attach(cl) > eda.shape(Age) > eda.shape(Height) > eda.shape(Weight) > tab.sex <- table(Sex) > barplot(tab.sex)
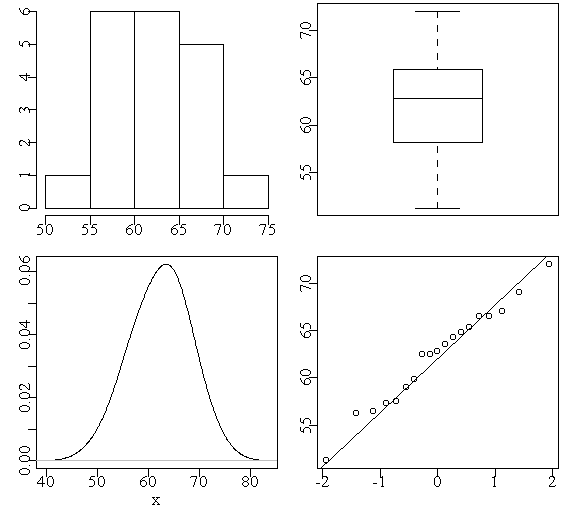
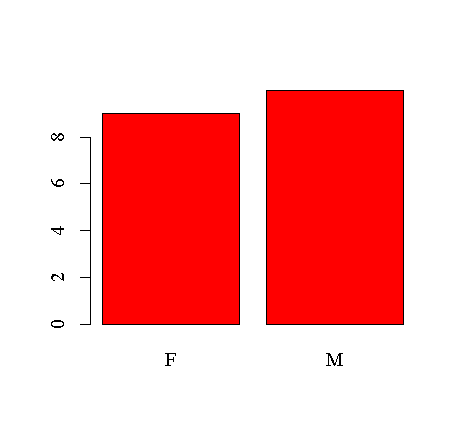
因为数据是不同个体的观测所以不可能有序列相关,未画时间序列图。这里给出了身高的分布图(图12)及性别的频数直方图。可以看出,身高和体重都相当接近正态且无明显的异常点,体重因为取离散值所以直方图不接近正态,但从核密度估计曲线看仍可作为正态处理。
要计算一些简单统计量,可以用summary()函数。
为了研究数值型变量Weight、Height、Age间的关系,我们画它们的散点图矩阵:
> pairs(cbind(Height, Weight, Age))
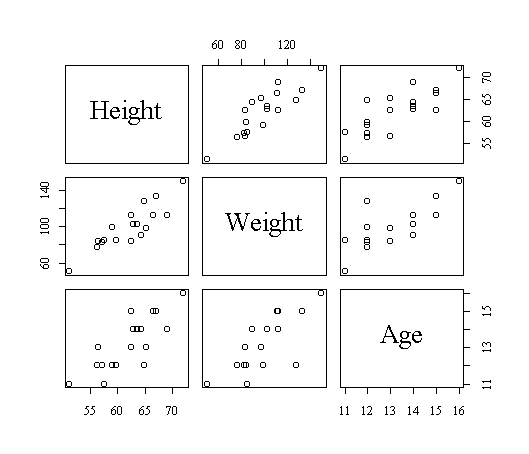
从散点图矩阵(图14)可以看出三个变量之间都可能有线性相关关系。
为了研究因子Sex对其它变量的影响,可以画Sex不同水平上各变量的盒形图,如:
> par(mfrow=c(1,3)) > boxplot(Weight ~ Sex, ylab="Weight") > boxplot(Height ~ Sex, ylab="Height") > boxplot(Age ~ Sex, ylab="Age")
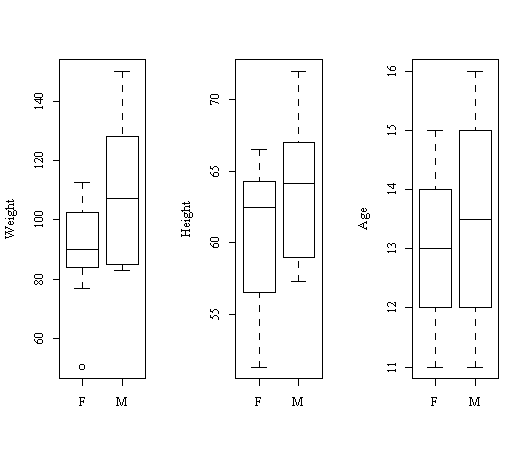
从图15可以看出,男女的体重、身高有明显的差别,而年龄则差别不明显。我们也可以分不同性别对某一变量分别作图或计算,这里只要使用向Weight[Sex=="F"],Weight[Sex=="M"] 这样的取子集的办法就可以把观测分组。更进一步还可以用函数tapply直接按一个因子对观测分组然后作用某个函数:
> tapply(Weight, Sex, hist)
为了研究因子Sex的不同水平对其它变量间的相关关系的影响,可以作协同图:
> coplot(Weight ~ Height | Sex)
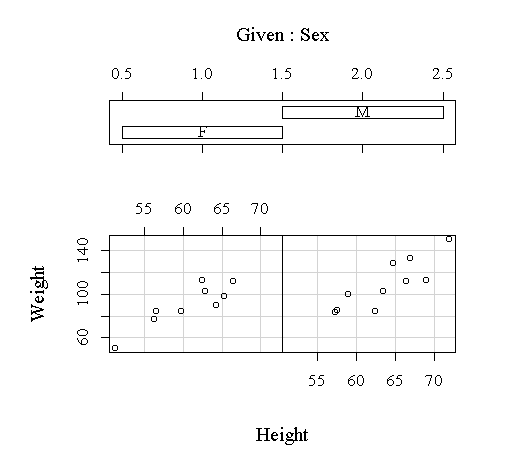
结果图16没有反映明显的差别。
我们来分析男女的身高有无显著差异,这是两组比较的问题。上面EDA部分的并排盒形图已经提示男女身高有明显差异,这里我们用统计假设检验给出统计结论。
男女两组可以认为是独立的,而且每组内的观测也可以认为是相互独立的。根据EDA 结果可以认为两组都来自正态总体。这样,我们可以使用两样本t检验。因为方差是否相等为止,我们干脆用不要求方差相等的近似两样本t检验:
> t.test(Height[Sex="F"], Height[Sex="M"])
Welch Two Sample t-test
data: Height[Sex == "F"] and Height[Sex == "M"]
t = -1.4513, df = 16.727, p-value = 0.1652
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-8.155098 1.512875
sample estimates:
mean of x mean of y
60.58889 63.91000
结果p值为0.1652,按我们一般采用的0.05水平是不显著的。所以从这组样本看男女的身高没有发现显著差异。
t.test也可以进行方差相等的两组比较,以及成对比较,单总体的均值检验,详见随机文档。
类似可以进行男女体重的比较,p值为0.06799,也不显著。
下面我们研究对体重的预报。从散点图矩阵看,体重与身高之间有明显的线性相关,所以我们先拟合一个体重对身高的一元线性回归模型:
> lm.fit1 <- lm(Weight ~ Height, data=cl)
> lm.fit1
Call:
lm(formula = Weight ~ Height, data = cl)
Coefficients:
(Intercept) Height
-143.027 3.899
> summary(lm.fit1)
Call:
lm(formula = Weight ~ Height, data = cl)
Residuals:
Min 1Q Median 3Q Max
-17.6807 -6.0642 0.5115 9.2846 18.3698
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -143.0269 32.2746 -4.432 0.000366 ***
Height 3.8990 0.5161 7.555 7.89e-07 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 11.23 on 17 degrees of freedom
Multiple R-Squared: 0.7705, Adjusted R-squared: 0.757
F-statistic: 57.08 on 1 and 17 degrees of freedom, p-value: 7.887e-007
拟合的模型方程为Weight = -143.0269 + 3.8990×Height,复相关系数平方为0.7705,检验模型的斜率为0的p值为7.887e-007,可见模型是显著的。对于一元回归,我们可以在因变量对自变量的散点图上叠加回归直线来看回归拟合的效果(图17):
> plot(Weight ~ Height)
> abline(lm.fit1)
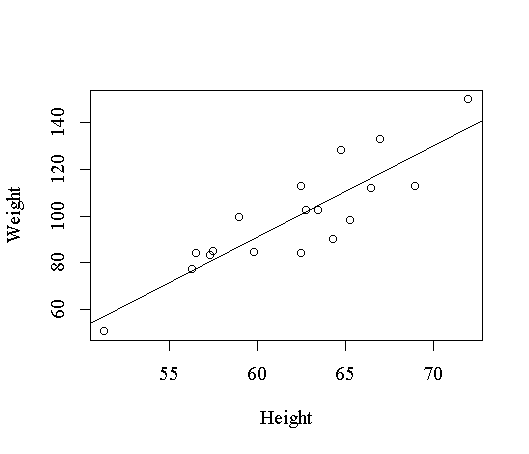
一般地,lm拟合结果对象的plot()函数可以作出若干张检查拟合效果的图形,R可以作四个图:残差对拟合值图、残差的正态概率图、标准化残差对拟合值图、Cook距离图。
> oldpar <- par(mfrow=c(2,2), mar=c(2,2,1.5,0.2), mgp=c(1.2, 0.2, 0)) > plot(lm.fit1) > par(oldpar)
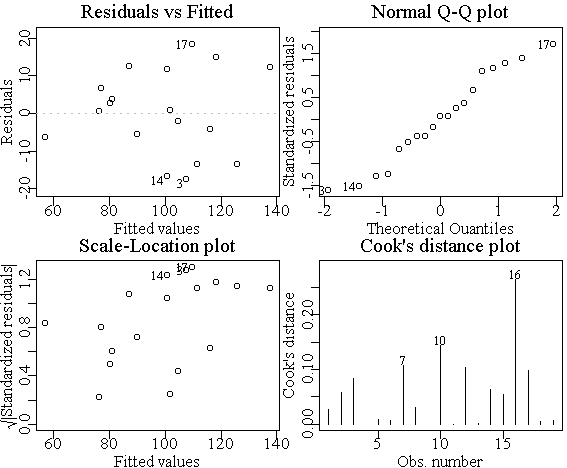
见图18。如果想每个图都用全窗口来看则不要设置图形参数。四个图中,残差对拟合值图可以反映残差中残留的结构,如果模型充分的话残差应该是随机变换没有任何模式的。残差的正态概率图可以检验线性回归假设检验的重要假定――误差项服从正态分布是否合理,可以看出残差的分布重尾、轻尾、左偏、右偏等情况。标准化残差平方根对拟合值图可以发现残差的异常值点,即拟合最差的点。Cook距离衡量每一观测对拟合结果的影响大小,数值大的为强影响点。图中自动标出了最突出的点。
从lm.fit1的回归诊断图看残差没有明显的模式,但残差分布有轻尾倾向。没有明显的异常值点。
下面我们看加入其它变量能否进一步改善模型的预报能力。用add1函数可以判断加入新的变量可以改善模型:
> add1(lm.fit1, ~ . + Age + Sex)
Single term additions
Model:
Weight ~ Height
Df Sum of Sq RSS AIC
<none> 2142.49 93.78
Age 1 22.39 2120.10 95.58
Sex 1 184.71 1957.77 94.07
>
add1的结果显示一个方差分析表,列出各行中<none>一行为不加变量的情况,Age 一行为加入一个变量Age后的情况,Sex一行为加入一个变量Sex的情况。各列中DF为此变量的自由度,Sum of Sq为该变量对应的平方和,RSS为加入该变量后的残差平方和,AIC为加入该变量后的AIC统计量值。AIC较小的模型为较好的,所以如果加入某个变量后的AIC减小就可以加入此变量。这里加入Age和加入Sex都使AIC变大,所以不应加入这两个变量。
如果一开始就加入了所有变量,可以用drop1()函数考察去掉一个变量后AIC是否可以变小:
> lm.fit2 <- lm(Weight ~ Height + Age + Sex, data=cl)
> summary(lm.fit2)
Call:
lm(formula = Weight ~ Height + Age + Sex, data = cl)
Residuals:
Min 1Q Median 3Q Max
-19.6540 -6.5737 0.4602 7.6708 20.8515
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -125.1151 33.9038 -3.690 0.00218 **
Height 2.8729 0.9971 2.881 0.01142 *
Age 3.1131 3.2362 0.962 0.35132
SexM 8.7443 5.8350 1.499 0.15472
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 11.09 on 15 degrees of freedom
Multiple R-Squared: 0.8025, Adjusted R-squared: 0.763
F-statistic: 20.31 on 3 and 15 degrees of freedom, p-value: 1.536e-005
> drop1(lm.fit2)
Single term deletions
Model:
Weight ~ Height + Age + Sex
Df Sum of Sq RSS AIC
<none> 1844.01 94.93
Height 1 1020.61 2864.62 101.30
Age 1 113.76 1957.77 94.07
Sex 1 276.09 2120.10 95.58
>
从summary()的结果看Age和Sex就不显著。用drop1()发现去掉Age可以使AIC从94.93变小为94.07,所以应该去掉Age。对去掉Age后的模型再用drop1()发现Sex也应该去掉。所以我们最后得到的模型时lm.fit1。
在修改模型或数据改变后重新拟合时还可以使用update函数,比如要从lm.fit2中去掉Age就可以用:
lm.fit3 <- update(lm.fit2, . ~ . - Age)
在自变量个数较多时S提供了一个step()函数用来进行逐步回归,它从一个初始模型开始自动判断增加或去掉变量,最后得到较好的模型:
> lm.step <- step(lm.fit0, ~ . + Height + Age + Sex)
Start: AIC= 119.75
Weight ~ 1
Df Sum of Sq RSS AIC
+ Height 1 7193.2 2142.5 93.8
+ Age 1 5124.5 4211.2 106.6
+ Sex 1 1681.1 7654.6 118.0
<none> 9335.7 119.7
Step: AIC= 93.78
Weight ~ Height
Df Sum of Sq RSS AIC
<none> 2142.5 93.8
+ Sex 1 184.7 1957.8 94.1
+ Age 1 22.4 2120.1 95.6
- Height 1 7193.2 9335.7 119.7
>
得到适当的模型以后,我们可以用模型进行拟合或预报。拟合只要对模型拟合结果用predict() 函数,如:
> predict(lm.fit1)
Alice Becka Gail Karen Kathy Mary Sandy
77.26829 111.57976 107.68073 76.48849 90.13509 116.25859 56.99333
Sharon Tammy Alfred Duke Guido James Jeffrey
100.66247 101.83218 126.00617 104.56150 118.20811 80.38752 100.66247
John Philip Robert Thomas William
87.01587 137.70326 109.63024 81.16732 116.25859
>
对新数据如果想作预报,可以在对predict加入新数据的数据框作为参数:
> new.data <- data.frame(Height=c(50, 51.2, 68, 69.7))
> predict(lm.fit1, new.data)
1 2 3 4
51.92459 56.60343 122.10714 128.73549