Section 5.5 Reflections
Example 5.57. Warm-up.
Suppose \(f(x)\) is given in the table below:
| \(x\) | \(f(x)\) |
| \(-1\) | \(2\) |
| \(0\) | \(3\) |
| \(1.3\) | \(-4\) |
| \(7\) | \(0\) |
| \(14\) | \(1\) |
Now, let's define a new function \(g(x)=-f(x)\text{.}\) We want to construct the table for \(g(x)\text{:}\)
| \(x\) | \(g(x)\) |
| \(-1\) | |
| \(0\) | |
| \(1.3\) | |
| \(7\) | |
| \(14\) |
To fill in the top row, we need to find \(g(-1)\text{.}\) Based on our definition of \(g(x)\text{,}\) we have that \(g(-1)=-f(-1)\text{.}\) From the table for \(f(x)\text{,}\) we know that \(f(-1)=2\text{.}\) Therefore,
We can fill out the rest of the table following the same logic:
| \(x\) | \(g(x)\) |
| \(-1\) | \(-2\) |
| \(0\) | \(-3\) |
| \(1.3\) | \(4\) |
| \(7\) | \(0\) |
| \(14\) | \(-1\) |
Now, let's define a new function \(h(x)=f(-x)\text{.}\) We want to construct the table for \(h(x)\text{.}\) Let's follow the same logic we had for \(g(x)\) above: to fill in the top row, we need to find \(h(-1)\text{.}\) Based on our definition of \(h(x)\text{,}\) we have that \(h(-1)=f(-(-1))=f(1)\text{.}\) However, at this point we are stuck, because \(x=1\) is not in our table for \(f(x)\text{.}\) So, we cannot use the same input values for \(h(x)\text{.}\) Instead, we need to reverse engineer what inputs we can use for \(h(x)\) that will match up to the inputs we have for \(f(x)\text{.}\) For example, we know what \(f(-1)\) is, and \(h(1)=f(-(1))=f(-1)\text{,}\) that means we can use \(1\) as one of our inputs for \(h(x)\) and we have that \(h(1)=2\text{.}\) We can follow the same logic to get the rest of the table:
| \(x\) | \(h(x)\) |
| \(1\) | \(2\) |
| \(0\) | \(3\) |
| \(-1.3\) | \(-4\) |
| \(-7\) | \(0\) |
| \(-14\) | \(1\) |
Let's compare the two functions we looked at in the warm-up example:
| \(x\) | \(f(x)\) | \(-f(x)\) |
| \(-1\) | \(2\) | \(-2\) |
| \(0\) | \(3\) | \(-3\) |
| \(1.3\) | \(-4\) | \(4\) |
| \(7\) | \(0\) | \(0\) |
| \(14\) | \(1\) | \(-1\) |
| \(x\) | \(f(-x)\) |
| \(1\) | \(2\) |
| \(0\) | \(3\) |
| \(-1.3\) | \(-4\) |
| \(-7\) | \(0\) |
| \(-14\) | \(1\) |
When we were looking at \(-f(x)\text{,}\) we multiplied the outside by \(-1\text{,}\) so we multiplied all of our outputs by \(-1\text{.}\) On the graph, remember that the outputs are the \(y\)-values, which makes this a vertical transformation. Since we flipped the sign of all of the \(y\)-values, so this would flip the graph up and down. On the other hand, when we were looking at \(f(-x)\text{,}\) we multiplied the inside by \(-1\text{,}\) so we multiplied all of our inputs by \(-1\text{.}\) On the graph, remember that the inputs are the \(x\)-values, which makes this a horizontal transformation. Since we flipped the sign of all of the \(x\)-values, so this would flip the graph left-to-right.
Definition 5.64. Reflections/Flips.
There are two possible reflections (sometimes called flips):
Vertical Reflection: The graph of \(-f(x)\) is the same as the graph of \(f(x)\text{,}\) but flipped vertically over the \(x\)-axis.
Horizontal Reflection: The graph of \(f(-x)\) is the same as the graph of \(f(x)\text{,}\) but flipped horizontally over the \(y\)-axis.
Note that when we say "flipped over the \(x\)-axis" or "flipped over the \(y\)-axis", you can think of it like putting a mirror on the axis, and the reflection you see in the mirror is the new graph.
See below for an animation of what this transformation does to a graph. If you want to see the animation in a larger window, click here 13 .
Example 5.65.
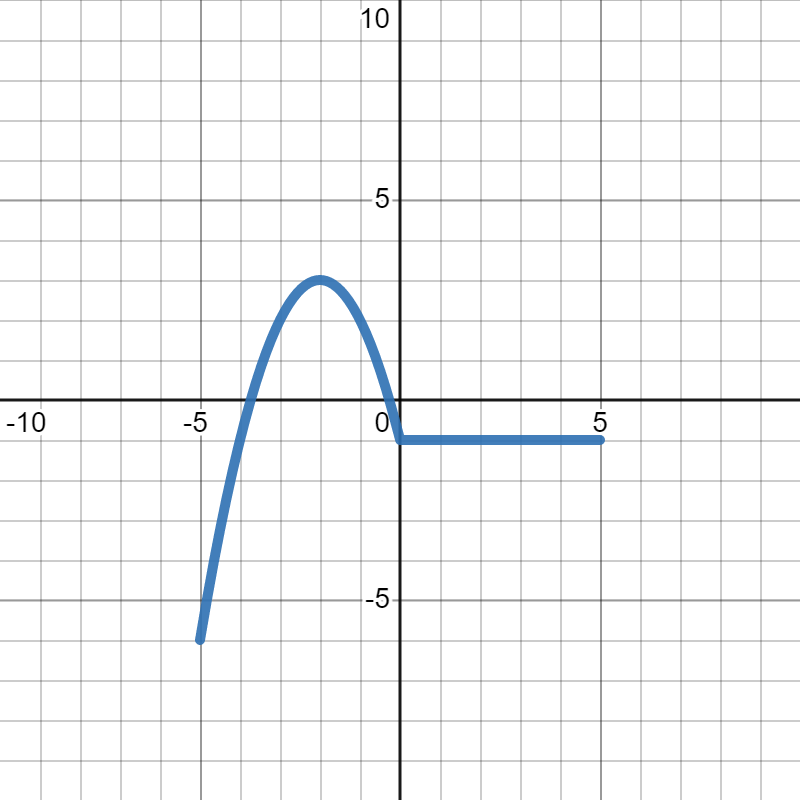
Below is the graph of \(h(x)\text{:}\)
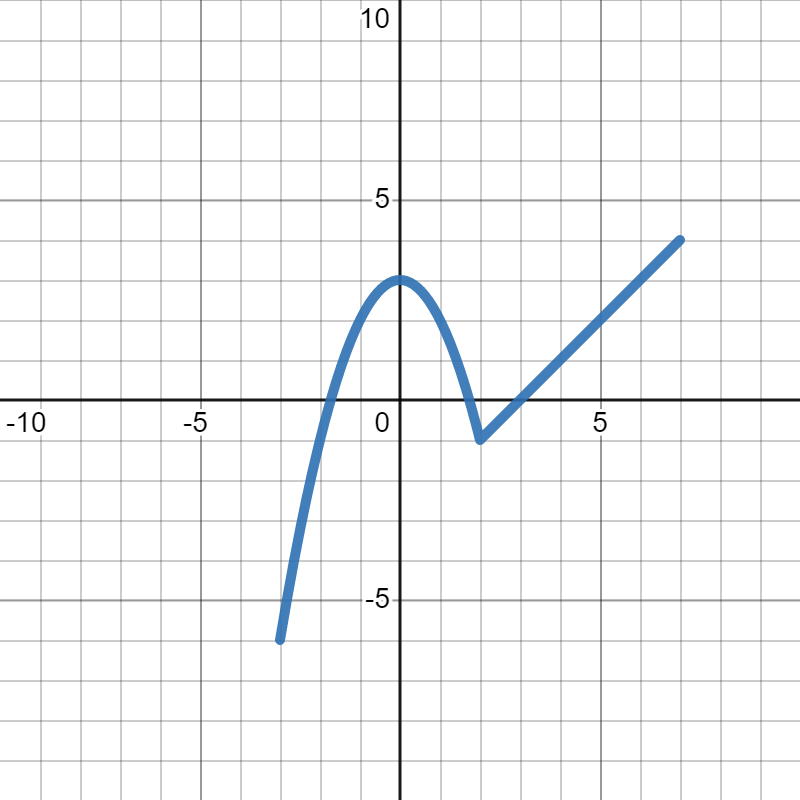
We want to figure out which of the following is the graph of \(-h(x)\text{.}\) In each, the gray dotted graph is the orignal graph of \(h(x)\) so you can more easily see how it changed.
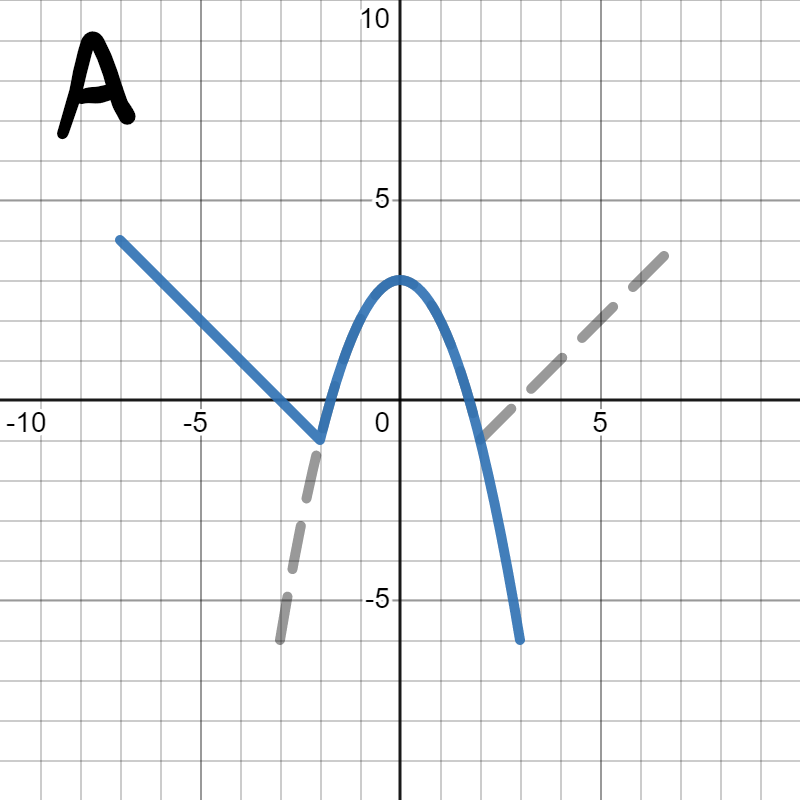
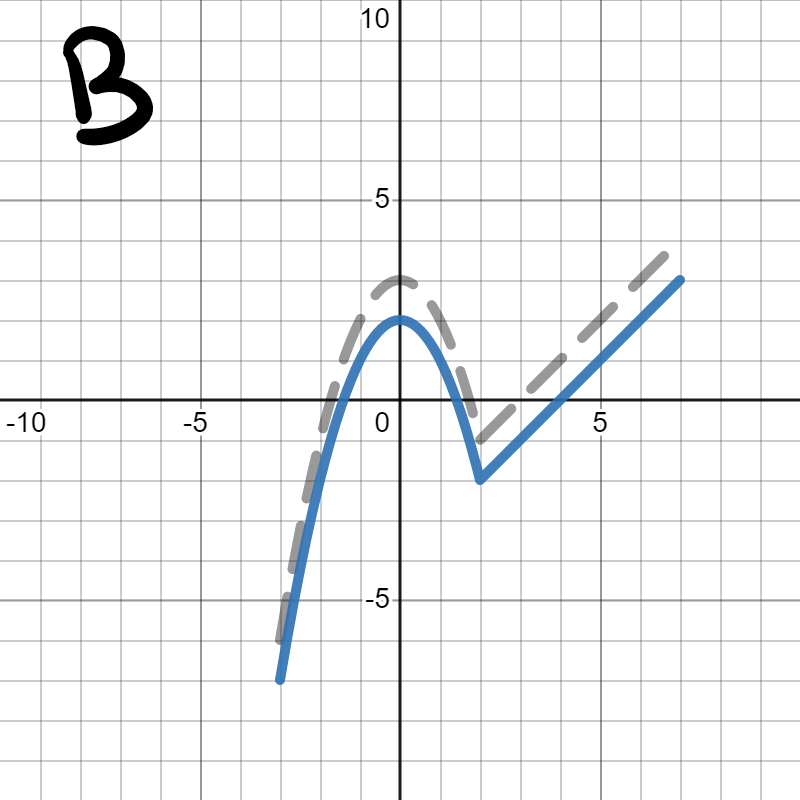
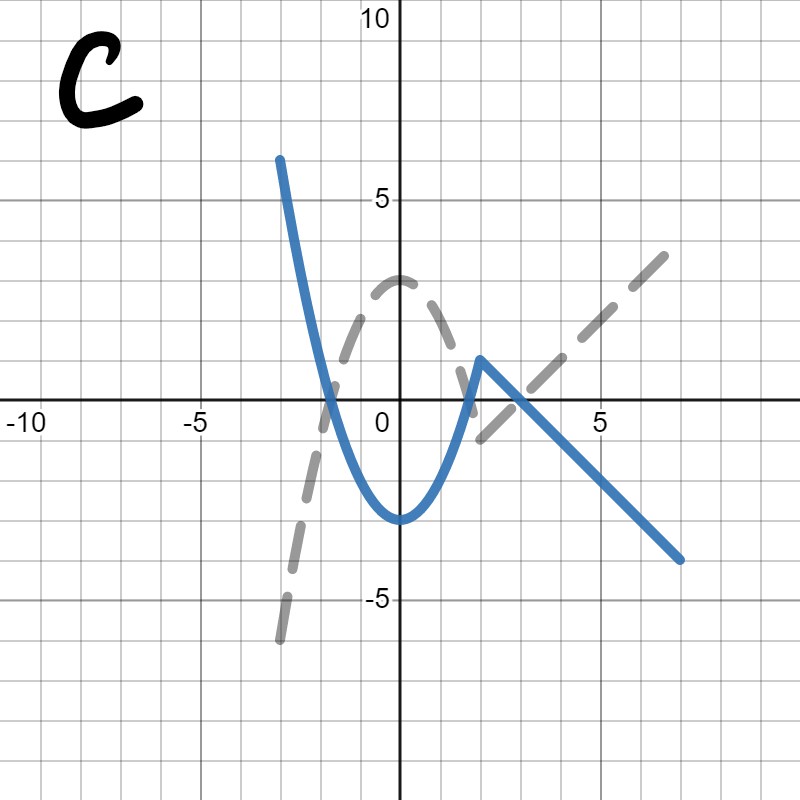
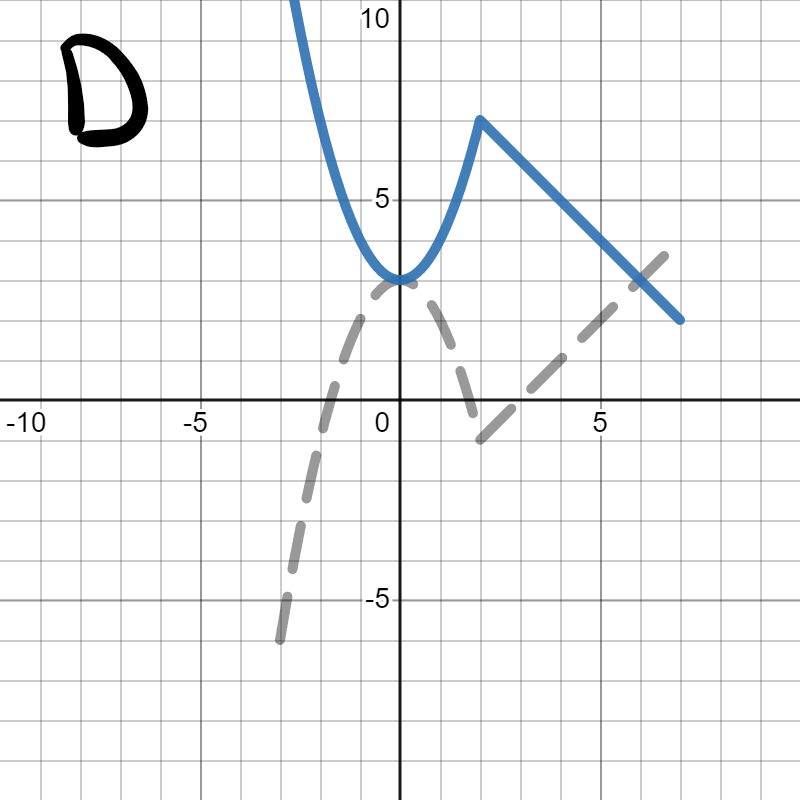
Since we are looking for \(-h(x)\text{,}\) we are looking for the graph to flip vertically (over the \(x\)-axis), which is graph C. Graph A flipped horizontally over the \(y\)-axis, which would be \(h(-x)\text{.}\) Graph B shifted down by 1, which we learned in Section 5.1 would be \(h(x)-1\text{.}\) Graph D is flipped upside down, but it's too high on the graph, since we want to flip over the \(x\)-axis. We'll learn about how to combine a flip and a shift in Section 5.6
Checkpoint 5.66.
The graph of \(p(x)\) is below:
Sketch the graph of each of the following:
\(\displaystyle -p(x)\)
\(\displaystyle p\left(-x\right)\)
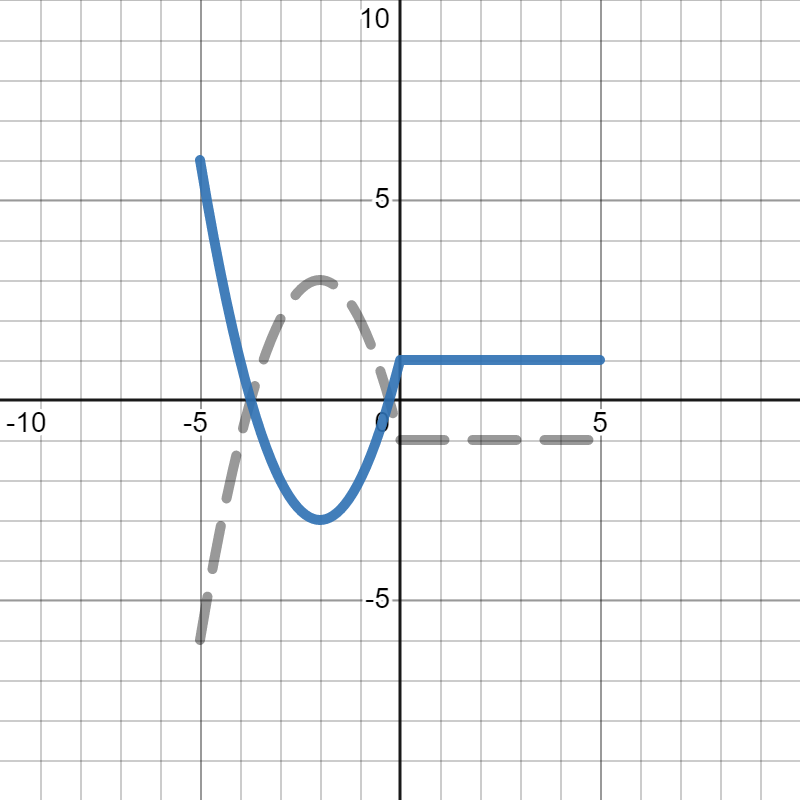
- To draw \(-p(x)\text{,}\) we see that we are flipping the graph vertically (over the \(x\)-axis). Since we are swapping the signs of all the \(y\)-values, and \(0\) times anything is still \(0\text{,}\) the points on the \(x\)-axis (where \(y=0\)) stay where they are at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-5,-6)\) on the original graph to \((-5,6)\text{.}\) Similarly, you would move the point \((-2,3)\) on the original graph to \((-2,-3)\text{,}\) move the point \((0,-1)\) on the original graph to \((0,1)\text{,}\) and move the point \((5,-1)\) on the original graph to \((5,1)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
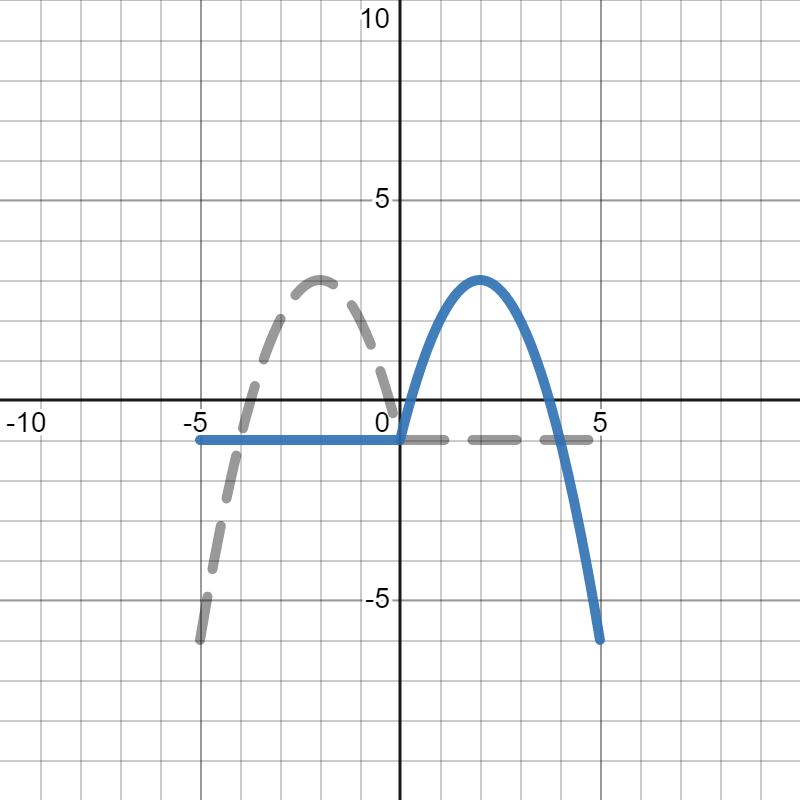
- To draw \(p(-x)\text{,}\) we see that we are flipping the graph horizontally (over the \(y\)-axis). Since we are swapping the signs of all the \(x\)-values, and \(0\) times anything is still \(0\text{,}\) the point on the \(y\)-axis (where \(x=0\)) stays where it is at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-5,-6)\) on the original graph to \((5,-6)\text{.}\) Similarly, you would move the point \((-2,3)\) on the original graph to \((2,3)\text{,}\) and move the point \((5,-1)\) on the original graph to \((-5,-1)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
Example 5.67.
Suppose \(f(x)=x^7-2x^4+5x^3-2x+6\) and \(g(x)\) is the same as \(f(x)\) but flipped vertically. Let's write a formula for \(g(x)\text{.}\) Since we are flipping vertically, that means we are multiplying by \(-1\) on the outside of the function.
What if we wanted to flip it horizontally instead? In that case, we would be multiplying by \(-1\) on the inside of the function.
Notice how we simplified in the equation above. Any negatives inside of an even power cancel out and don't do anything. However, the negatives in the odd powers do not cancel, so they flip signs.
Checkpoint 5.68.
Suppose \(f(x)=3x^8+4x^7-x^6-5x^5+x^3-7x^2+8\text{.}\)
Suppose \(g(x)\) is the same as \(f(x)\) but flipped vertically. Write a formula for \(g(x)\text{.}\)
Suppose \(h(x)\) is the same as \(f(x)\) but flipped horizontally. Write a formula for \(h(x)\text{.}\)
\(\displaystyle g(x)=-3x^8-4x^7+x^6+5x^5-x^3+7x^2-8\)
\(\displaystyle h(x)=3x^8-4x^7+x^6+5x^5-x^3-7x^2+8\)
-
Since we are flipping vertically, that means we are multiplying by \(-1\) on the outside of the function.
\begin{equation*} g(x)=-f(x)=-(3x^8+4x^7-x^6-5x^5+x^3-7x^2+8)=-3x^8-4x^7+x^6+5x^5-x^3+7x^2-8 \end{equation*} -
Since we are flipping horizontally, that means we are multiplying by \(-1\) on the inside of the function.
\begin{align*} h(x)\amp=f(-x)\\ \amp=3(-x)^8+4(-x)^7-(-x)^6-5(-x)^5+(-x)^3-7(-x)^2+8\\ \amp= 3x^8-4x^7+x^6+5x^5-x^3-7x^2+8 \end{align*}Notice how we simplified in the equation above. Any negatives inside of an even power cancel out and don't do anything. However, the negatives in the odd powers do not cancel, so they flip signs.
https://www.desmos.com/calculator/gnzbeb56rf