


Next: Finite series formulas.
Up: formulas
Previous: formulas
Let 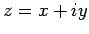 be a complex number.
be a complex number.
- The conjugate
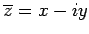 .
.
The real part
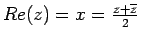 .
.
The imaginary part
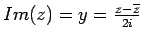 .
.
The norm
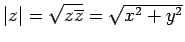 .
.
- The reciprocal
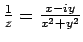 .
.
- The direction from
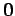 (for a non zero
(for a non zero 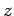 )
)
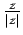 .
.
- The Euler representation.
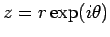 where
where 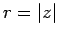 and
and
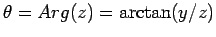 . The angle
. The angle 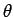 can be replaced by
any angle in the set
can be replaced by
any angle in the set
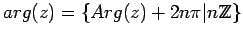 .
.
Avinash Sathaye
2007-08-09
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.