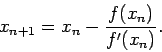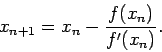Next: About this document ...
Up: formulas
Previous: Trigonometry
- If
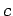 is a constant, then
is a constant, then 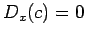 .
Moreover,
.
Moreover,
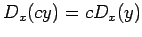 .
.
-
- For any real
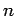 ,
,
As a special case:
-
-
- Linear approximation formula: Linear approximation
to
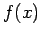 at
at 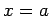 is:
is:
- Newton's Method for finding a root.
Change the current guess
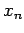 to
to
Avinash Sathaye
2007-08-09