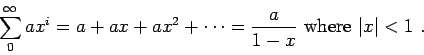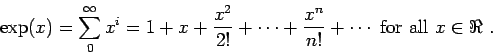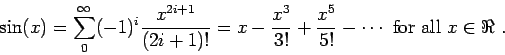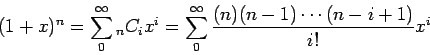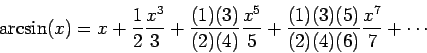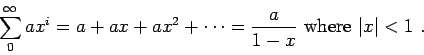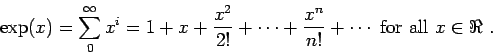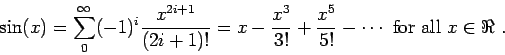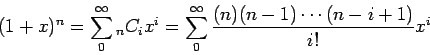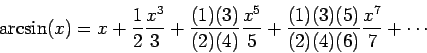Next: Geometry.
Up: formulas
Previous: Finite series formulas.
- Geometric series
- Exponential series
- Basic Trigonometric series
- Generalized Binomial series
where 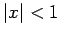 or
or 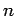 is a non negative integer and
is a non negative integer and 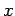 is any complex number.
is any complex number.
- Log series
- Arctan series
where 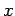 is real with
is real with 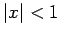 .
.
- Arcsine series
where 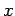 is real with
is real with 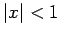 .
.
Avinash Sathaye
2007-08-09