- The determinant of a
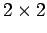 matrix:
matrix:
- Cramer's Rule: To solve
define:
If 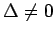 then the answer is
then the answer is
If 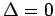 and at least one of
and at least one of
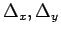 is non zero then
there is no solution.
is non zero then
there is no solution.
If all
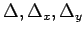 , then there are infinitely many
solutions.
, then there are infinitely many
solutions.
- The distance between two points A and B on the real line is
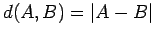 .
.
- For two points
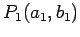 and
and 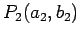 in the xy-plane:
in the xy-plane:
- The distance between the points is
- The parametric two point form of the line containing these
points is
- The compact parametric two point form of the line is
- The midpoint of two points
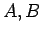 is
is
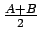 .
.
- The two point form of the equation through the points
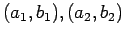 is
is
- The slope of the line through two points
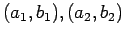 is
is
where the slope is infinite and the line is vertical if 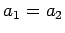 .
.
- The slope intercept form of the line joining
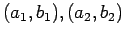 is
is 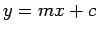 where
where 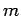 is the slope and
is the slope and
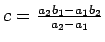 is the y-intercept.
is the y-intercept.
- If
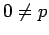 is the
is the 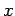 intercept and
intercept and 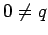 is the
is the
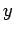 -intercept,
then the line is:
-intercept,
then the line is:
- A line parallel to
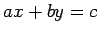 is
is 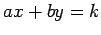 for some
for some 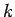 .
.
- A line perpendicular to
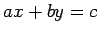 is
is 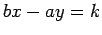 for some
for some 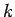 .
.
- The quadratic function
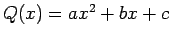 has extremum value at
has extremum value at
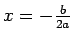 . The value is
. The value is
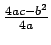 . It is a maximum if
. It is a maximum if
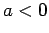 and minimum if
and minimum if 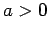 .
.
- The equation
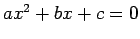 with
with 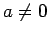 has solutions:
has solutions:
- The equation of a circle with center
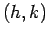 and radius
and radius 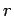 is
is
- For the circle
the center is 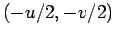 and radius is
and radius is
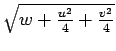 .
.
- A parametric form of the circle
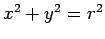 is:
is:
where 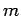 is the parameter.
is the parameter.
The trigonometry parameterization for the same circle is:
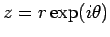 or
or
with parameter 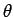 .
.
- A circle with diameter
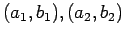 is:
is:
- The distance from a point
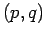 to the line
to the line 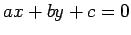 is:
is:
The expression 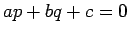 if and only if the point lies on the line.
if and only if the point lies on the line.
Moreover, the sign of the expression 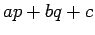 changes if the point
moves from one side of the line to the other.
changes if the point
moves from one side of the line to the other.
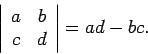
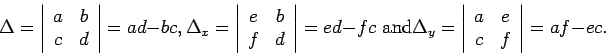
![]() then the answer is
then the answer is
![]() and at least one of
and at least one of
![]() is non zero then
there is no solution.
is non zero then
there is no solution.
![]() , then there are infinitely many
solutions.
, then there are infinitely many
solutions.

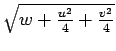 .
.
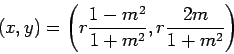
![]() or
or
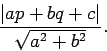
![]() if and only if the point lies on the line.
if and only if the point lies on the line.
![]() changes if the point
moves from one side of the line to the other.
changes if the point
moves from one side of the line to the other.