Section 8.1 Interval Notation
Subsection 8.1.1 Endpoints
Writing an interval in interval notation looks a lot like writing an ordered pair for a point on a graph. It will be two numbers, separated by a comma, with some sort of parentheses surrounding it. In an interval, we always write the smaller endpoint first, and we use either round parentheses () or square brackets [] to indicate whether the endpoint is included or not.
| Not Included | \(\lt \) or \(\gt \) | ( or ) |
| Included | \(\le\) or \(\ge\) | [ or ] |
Example 8.1.3.
Let’s look at the example we started this section with: all of the numbers between 2 and 7, including 2 but not including 7. Since we want the numbers between 2 and 7, those are our enpoints. Since we are including 2, it’s going to have a square bracket [. Since we are not incluidng 7, it is going to have a round parentheses ). We always write the smaller endpoint first, so in interval notation, we would have \([2,7)\text{.}\)
Checkpoint 8.1.4.
Write each of the following using interval notation:
-
All numbers between \(-1\) and \(3\text{,}\) including both endpoints.
-
\(\displaystyle 0\le x \lt 9\)
-
\(\displaystyle -10 \lt x \lt 10\)
Solution.
Write each of the following using interval notation:
-
All numbers between \(-1\) and \(3\text{,}\) including both endpoints. Since we want the numbers between \(-1\) and \(3\text{,}\) those are our enpoints. Since we are including both endpoints, they are going to have square brackets []. We always write the smaller endpoint first, so in interval notation, we would have \([-1,3]\text{.}\)
-
\(0\le x \lt 9\text{.}\) Since we want the numbers between 0 and 9, those are our enpoints. Since we are including 0, it’s going to have a square bracket [. Since we are not incluidng 9, it is going to have a round parentheses ). We always write the smaller endpoint first, so in interval notation, we would have \([0,9)\text{.}\)
-
\(-10 \lt x \lt 10\text{.}\) Since we want the numbers between \(-10\) and \(10\text{,}\) those are our enpoints. Since we are not including either endpoint, they are going to have round parentheses ()). We always write the smaller endpoint first, so in interval notation, we would have \((-10,10)\text{.}\)
Subsection 8.1.2 Unbounded Intervals
Sometimes, our interval might go on forever in one direction. Even though there isn’t an endpoint, we can’t leave that side blank. So, we use \(\infty\) or \(-\infty\) as the placeholder. You might find it helpful to think of \(-\infty\) and \(\infty\) as the endpoints of the whole number line. However, since they aren’t actual numbers, they are never included. Therefore they always get round parentheses () in our interval notation.
Example 8.1.5.
Suppose we want to write \(x\gt 2\) in interval notation. We know that 2 is one of our endpoints, but the other side goes on forever. You might find it helpful to draw a number line to determine which side of 2 we want to include. In our case, this is what that would look like:
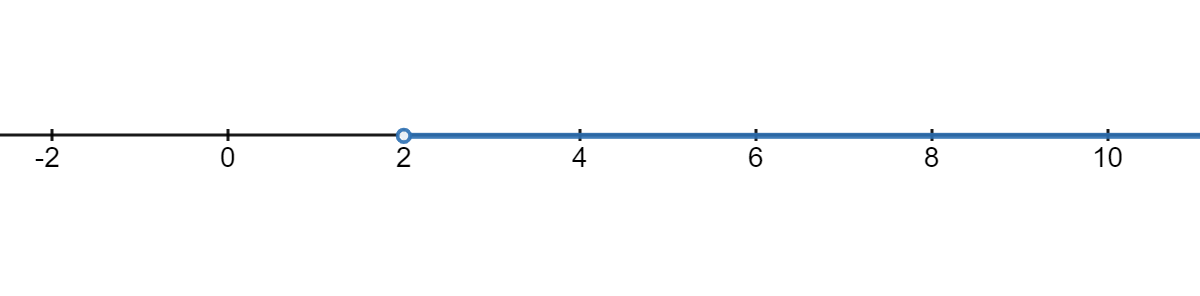
Since the interval goes on forever in the positive direction, we can think of \(\infty\) as the other endpoint. However, since \(\infty\) isn’t an actual number, it will always get a round parentheses ). Since the endpoint 2 is not included, it will also get a round parentheses (. So, in interval notation, our answer would be \((2,\infty)\text{.}\)
Checkpoint 8.1.6.
Write each of the following in interval notation:
-
All numbers less than 7
-
\(\displaystyle x\le -3.7\)
-
All positive numbers
Answer.
Solution.
Write each of the following in interval notation:
-
All numbers less than 7. Here is what that would look like on a number line:
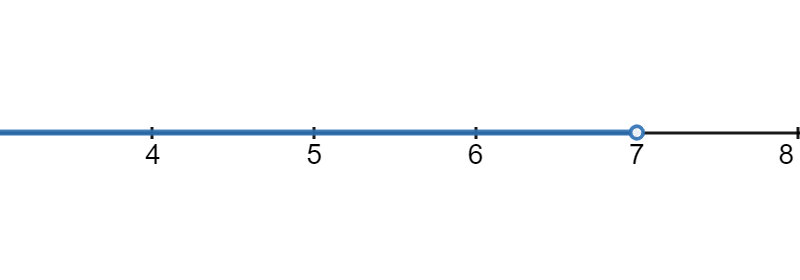 Since the interval goes on forever in the negative direction, we can think of \(-\infty\) as the other endpoint. However, since \(-\infty\) isn’t an actual number, it will always get a round parentheses (. Since the endpoint 7 is not included, it will also get a round parentheses ). So, in interval notation, our answer would be \((-\infty,7)\text{.}\)
Since the interval goes on forever in the negative direction, we can think of \(-\infty\) as the other endpoint. However, since \(-\infty\) isn’t an actual number, it will always get a round parentheses (. Since the endpoint 7 is not included, it will also get a round parentheses ). So, in interval notation, our answer would be \((-\infty,7)\text{.}\) -
\(x\le -3.7\text{,}\) here is what that would look like on a number line:
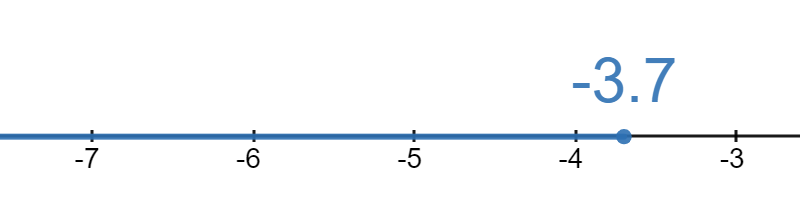 Since the interval goes on forever in the negative direction, we can think of \(-\infty\) as the other endpoint. However, since \(-\infty\) isn’t an actual number, it will always get a round parentheses (. Since the endpoint \(-3.7\) is included, it will get a square bracket ]. So, in interval notation, our answer would be \((-\infty, -3.7])\text{.}\)
Since the interval goes on forever in the negative direction, we can think of \(-\infty\) as the other endpoint. However, since \(-\infty\) isn’t an actual number, it will always get a round parentheses (. Since the endpoint \(-3.7\) is included, it will get a square bracket ]. So, in interval notation, our answer would be \((-\infty, -3.7])\text{.}\) -
All positive numbers means all numbers greater than 0, so here is what that would look like on a number line:
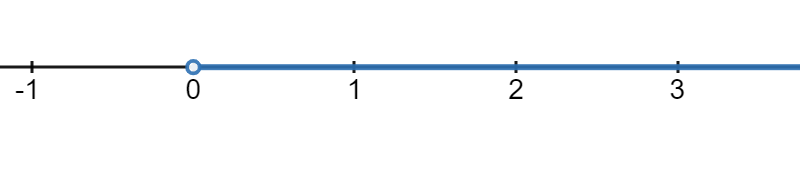 Since the interval goes on forever in the positive direction, we can think of \(\infty\) as the other endpoint. However, since \(\infty\) isn’t an actual number, it will always get a round parentheses ). Since the endpoint 0 is not included, it will also get a round parentheses (. So, in interval notation, our answer would be \((0,\infty)\text{.}\)
Since the interval goes on forever in the positive direction, we can think of \(\infty\) as the other endpoint. However, since \(\infty\) isn’t an actual number, it will always get a round parentheses ). Since the endpoint 0 is not included, it will also get a round parentheses (. So, in interval notation, our answer would be \((0,\infty)\text{.}\)
Subsection 8.1.3 Combining Intervals
When we want to put together more than one interval, we combine them with a union. When we are writing or typing, we just write a \(\cup\) between them.
Example 8.1.7.
Suppose we are working on a problem, and our answer has to include both the interval \(3 \lt x \le 8\) and the interval \(x \gt 10\text{.}\) First, we write each interval using interval notation, then we will combine them with a union. Using what we learned above, we know that \(3 \lt x \le 8\) is written as \((3,8]\text{,}\) and \(x \gt 10\) is written as \((10,\infty)\text{.}\) Since we want our answer to include both, our final answer is \((3,8]\cup(10,\infty)\text{.}\)
Example 8.1.8. Special Case: Everything Except a Number.
Suppose we wanted our answer to be everything except 3. That means we want to include all the numbers less than 3 and all the numbers greater than 3. That’s two intervals that we’ll combine with a union. All the numbers less than 3 is written as \((-\infty, 3)\text{,}\) and all the numbers greater than 3 is written as \((3,\infty)\text{.}\) Therefore, our final answer is \((-\infty, 3)\cup(3,\infty)\text{.}\)
Checkpoint 8.1.9.
Write each of the following in interval notation:
-
\(x \lt -1\) or \(x \ge 4\)
-
\(\displaystyle x \neq 42\)
-
Everything except \(\pm 2\) (Hint: You will probably find it helpful to draw a number line for this one).
Answer.
Solution.
Write each of the following in interval notation:
-
\(x \lt -1\) or \(x \ge 4\text{:}\) First, we know that \(x \lt -1\) is written as \((-\infty, -1)\text{,}\) and that \(x \ge 4\) is written as \([4,\infty)\text{.}\) Since our answer needs to include both possibilities, we combine them with a union to get our final answer of \((-\infty,-1)\cup[4,\infty)\text{.}\)
-
\(x \neq 42\text{:}\) That means we want to include all the numbers less than 42 and all the numbers greater than 42, just not 42 itself. That’s two intervals that we’ll combine with a union. All the numbers less than 42 is written as \((-\infty, 42)\text{,}\) and all the numbers greater than 42 is written as \((42,\infty)\text{.}\) Therefore, our final answer is \((-\infty, 42)\cup(42,\infty)\text{.}\)
-
Everything except \(\pm 2\text{.}\) Since this one is everything except two numbers (\(-2\) and \(2\)), it is easiest to start by drawing a number line:
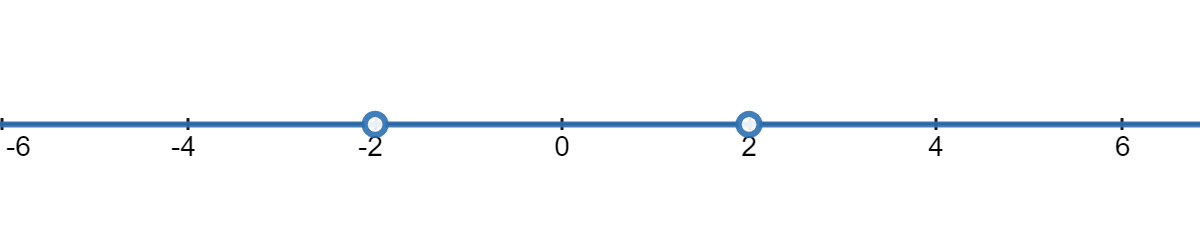 From the picture, we see that there are three intervals we need to work with: everything less than \(-2\text{,}\) everything between \(-2\) and \(2\text{,}\) and everything greater than \(2\text{.}\) In interval notation, those would each be \((-\infty, -2)\text{,}\) \((-2,2)\text{,}\) and \((2,\infty)\text{,}\) respectively. Therefore, our final answer to this question is \((-\infty, -2)\cup(-2,2)\cup(2,\infty)\text{.}\)
From the picture, we see that there are three intervals we need to work with: everything less than \(-2\text{,}\) everything between \(-2\) and \(2\text{,}\) and everything greater than \(2\text{.}\) In interval notation, those would each be \((-\infty, -2)\text{,}\) \((-2,2)\text{,}\) and \((2,\infty)\text{,}\) respectively. Therefore, our final answer to this question is \((-\infty, -2)\cup(-2,2)\cup(2,\infty)\text{.}\)
