Definition 10.1.1.
The roots of a polynomial are the \(x\)-values of the \(x\)-intercepts. We also sometimes call these the zeros of the function.
Section 10.1 Roots of Polynomials
Example 10.1.2.
Suppose \(f(x)\) is the polynomial graphed below. We want to find the roots of that function.
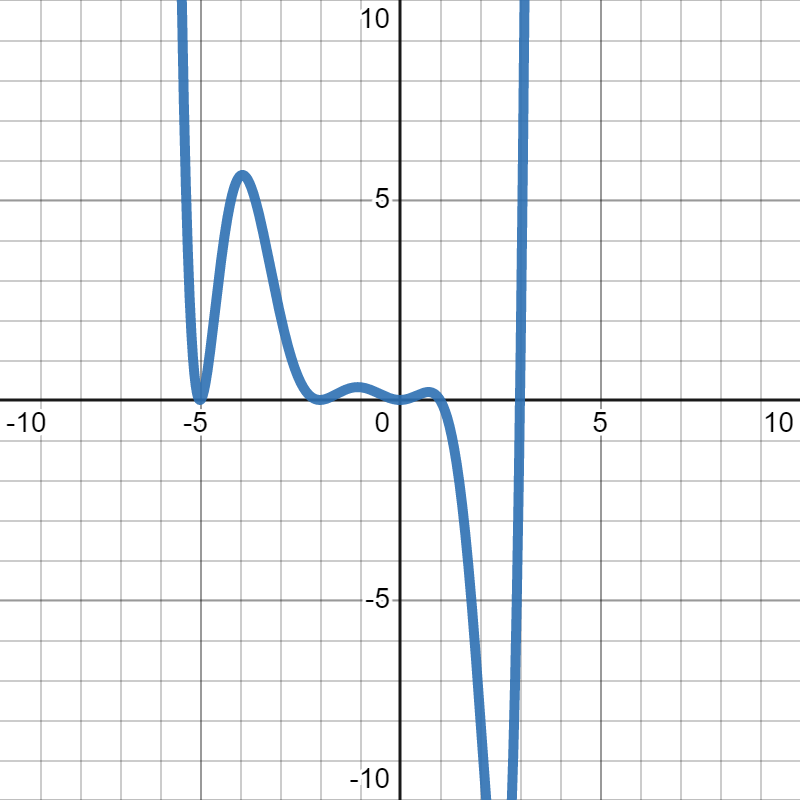
We look at the \(x\)-axis, which crosses the graph at \(x=-5, -2, 0, 1\) and \(3\text{,}\) so those are our roots. The answer to this question is \(x=-5, -2, 0, 1, 3\text{.}\)
Checkpoint 10.1.3.
Suppose \(f(x)\) is the polynomial graphed below. What are the roots of that function?
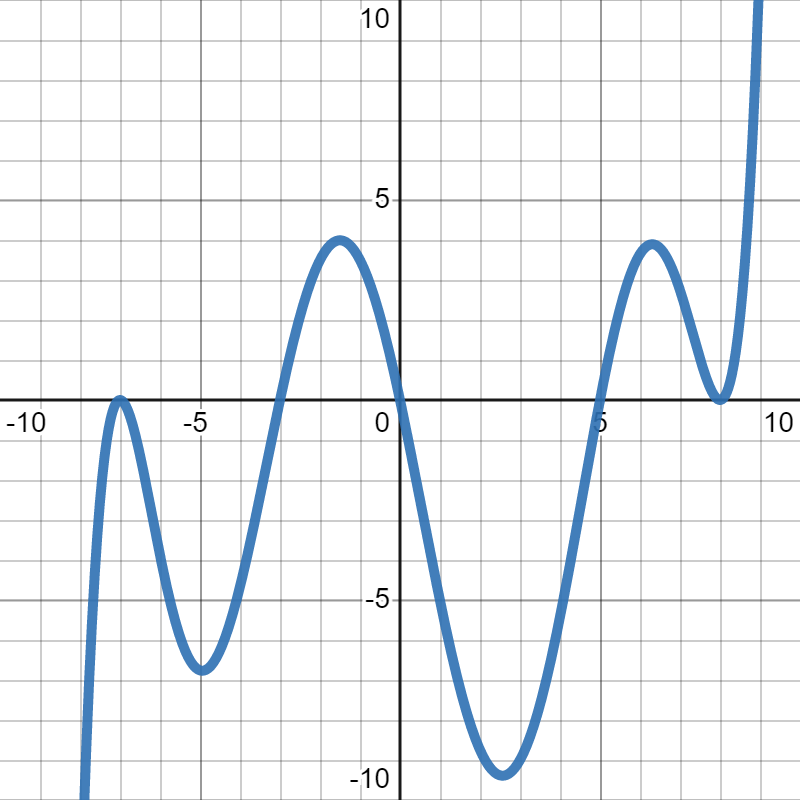
Answer.
\(x=-7, -3, 0, 5, 8\)
Solution.
To find the roots, we need to look at the \(x\)-axis. We see that it crosses the graph at \(x=-7, -3, 0, 5\text{,}\) and \(8\text{.}\) Therefore, the answer to this question is \(x=-7, -3, 0, 5, 8\text{.}\)
Most of the time, we will be given an equation for the function, and we will need to do algebra to figure out what the roots are, rather than looking at a graph. Since we are just looking for the \(x\)-intercepts, we know from Section 1.2 just need to set \(y=0\) and solve for \(x\text{.}\) There are lots of ways to solve polynomial equations but they get extremely complicated very quickly! In this class, we will only use the most straghtforward strategy, which works every time:
Example 10.1.4. Zero Product Property.
Suppose \(f(x)=-3x^4(x+5)^3(x-2)^7(x+8)^2\text{,}\) and we want to find its roots. As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:
\begin{equation*}
0=-3x^4(x+5)^3(x-2)^7(x+8)^2
\end{equation*}
Take a close look at the equation: we have a bunch of things multiplied together and it all equals 0. The fact that it equals 0 is special. There is no way to mulitply things together to get 0, unless one of the numbers you multiplied was already 0.
Why does that matter? Because we know one of the things we multiplied had to be 0 to begin with, this lets us separate our first equation into five separate equations:
\begin{align*}
0\amp=-3\\
0\amp=x^4\\
0\amp=(x+5)^3\\
0\amp=(x-2)^7\\
0\amp=(x+8)^2
\end{align*}
The first equation doesn’t have any \(x\) in it, and is nonsense since 3 does not equal 0. So that one doesn’t help us, we’ll ignore it. For the other four, we take roots and then add or subtract to solve. Since any root of 0 is still 0, we have four roots: \(x=0, -5, 2\text{,}\) and \(-8\text{.}\)
Checkpoint 10.1.5.
Answer.
\(x=-7, 2, 5, -1, -9\)
Solution.
As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:
\begin{equation*}
0=-\frac{1}{2}(x+7)^3(x-2)^2(x-5)^7(x+1)^3(x+9)^9
\end{equation*}
Just as we had with the example, we have a bunch of things multiplied together to be 0. That means one of them had to be zero to begin with. Because we know one of the things we multiplied had to be 0 to begin with, this lets us separate our first equation into six separate equations:
\begin{align*}
0\amp=-\frac{1}{2}\\
0\amp=(x+7)^3\\
0\amp=(x-2)^2\\
0\amp=(x-5)^7\\
0\amp=(x+1)^3\\
0\amp=(x+9)^9
\end{align*}
The first equation doesn’t have any \(x\) in it, and is nonsense since \(-\frac{1}{2}\) does not equal 0. So that one doesn’t help us, we’ll ignore it. For the other five, we take roots and then add or subtract to solve. Since any root of 0 is still 0, we have five roots: \(x=-7, 2, 5, -1\text{,}\) and \(-9\text{.}\)
Subsection 10.1.1 Multiplicity
Definition 10.1.6.
If \(f(x)\) is a polynomial with a root \(x=r\text{,}\) then it has a factor of \((x-r)\text{.}\)
Definition 10.1.7.
The multiplicity of a root of a polynomial is the number of times it is repeated. From the formula, we can tell the multiplicity by the power on the factor.
Example 10.1.8.
Let’s look at the function we had before: \(f(x)=-3x^4(x+5)^3(x-2)^7(x+8)^2\text{.}\) We already know that it has roots \(x=0, -5, 2\text{,}\) and \(-8\text{.}\) To find the multiplicities, we just have to take the exponents of the factors that go with them. We can summarize this information in a table, like the one below:
| Root | Multiplicity |
| \(0\) | \(4\) |
| \(-5\) | \(3\) |
| \(2\) | \(7\) |
| \(-8\) | \(2\) |
Checkpoint 10.1.10.
Answer.
| Root | Multiplicity |
| \(-7\) | \(3\) |
| \(2\) | \(2\) |
| \(5\) | \(7\) |
| \(-1\) | \(3\) |
| \(-9\) | \(9\) |
Solution.
We already know that it has roots \(x=-7, 2, 5, -1\text{,}\) and \(-9\text{.}\) To find the multiplicities, we just have to take the exponents of the factors that go with them. We can summarize this information in a table, like the one below:
| Root | Multiplicity |
| \(-7\) | \(3\) |
| \(2\) | \(2\) |
| \(5\) | \(7\) |
| \(-1\) | \(3\) |
| \(-9\) | \(9\) |
Now that we know how to find multiplicity from an equation, the logical question is: how do we find the multiplicity from a graph? The short answer is that you can’t! Lots of different multiplicities look exactly the same on the graph, so we cannot tell the exact number of the multiplicity from the graph alone. However, we are not out of luck entirely. We can tell some information about the multiplicity from the graph.
Fact 10.1.13. Multiplicity from a Graph.
-
A root with even multiplicity bounces off of the \(x\)-axis.
-
A root with odd multiplicity goes through the \(x\)-axis.
That is the only information about the multiplicity we can tell from a graph. That means that if you are given just a graph and asked for the multiplicities, the answer is either the word "even" or "odd", the answer is not a number. We cannot tell the difference on a graph between multiplicity 2, 4, or 100, but we can tell the difference between 2 and 3.
Example 10.1.14.
Suppose \(f(x)\) is the polynomial graphed below. We want to find the roots of that function and their multiplicities.
We look at the \(x\)-axis, which crosses the graph at \(x=-5, -2, 0, 1\) and \(3\text{,}\) so those are our roots. Now, to find the multiplicity, we have to look at whether it bounces off the \(x\)-axis or crosses it. We can put all that information into the following table:
| Root | Multiplicity |
| \(-5\) | even |
| \(-2\) | even |
| \(0\) | even |
| \(1\) | odd |
| \(3\) | odd |
Checkpoint 10.1.16.
Suppose \(f(x)\) is the polynomial graphed below. What are the roots of that function and their multiplicities?
Answer.
| Root | Multiplicity |
| \(-7\) | even |
| \(-3\) | odd |
| \(0\) | odd |
| \(5\) | odd |
| \(8\) | even |
Solution.
We look at the \(x\)-axis, which crosses the graph at \(x=-7, -3, 0, 5\) and \(8\text{,}\) so those are our roots. Now, to find the multiplicity, we have to look at whether it bounces off the \(x\)-axis or crosses it. We can put all that information into the following table:
| Root | Multiplicity |
| \(-7\) | even |
| \(-3\) | odd |
| \(0\) | odd |
| \(5\) | odd |
| \(8\) | even |
