Skip to main content

Section 4.1 Evaluating Inverse Functions

Section 2.5

Definition 4.1.1.

For a function \(f(x)\text{,}\) its inverse function (written \(f^{-1}(x)\) and pronounced "f inverse of x") is the function that swaps the roles of inputs and outputs for \(f(x)\text{.}\) In other words, if \(f(a)=b\text{,}\) then \(f^{-1}(b)=a\) and vise versa.
While it is possible to find a general formula for the inverse function, we leave that for the next section. For now, we will only focus on evaluating the inverse function at a given number. Luckily, this is exactly the same thing you did in section Section 2.5. The only difference is that we are now using new vocabulary and notation to state the question.

Example 4.1.2.

Suppose \(f(x)=\dfrac{x+1}{2x-3}\text{,}\) and we want to find \(f^{-1}(5)\text{.}\) We can see that \(5\) is the input to the inverse function, but because the inverse swaps inputs and outputs, that means that \(5\) is the output to the original function. So, we are trying to solve \(f(x)=5\text{:}\)
\begin{align*} f(x) \amp = 5\\ \dfrac{x+1}{2x-3} \amp = 5\\ x+1 \amp = 5(2x-3)\\ x+1 \amp 10x - 15\\ 1 \amp = 9x - 15 \\ 16 \amp = 9x \\ \frac{16}{9} = x \end{align*}
Therefore, our final answer is \(f^{-1}(x)=\frac{16}{9}\text{.}\)

Checkpoint 4.1.3.

  1. Suppose \(f(x)=3x-7\text{.}\) Evaluate \(f^{-1}(4)\text{.}\)
  2. Suppose \(g(x)=\dfrac{x}{x+3}\text{.}\) Evaluate \(g^{-1}(-4)\text{.}\)
  3. Suppose \(h(x)=x^3+1\text{.}\) Evaluate \(h^{-1}(9)\text{.}\)
Answer.
  1. \(\displaystyle f^{-1}(4)=\frac{11}{3}\)
  2. \(\displaystyle g^{-1}(-4)=\frac{-12}{5}\)
  3. \(\displaystyle h^{-1}(9)=2\)
Solution.
  1. Since \(f(x)=3x-7\) and we want to evaluate \(f^{-1}(4)\text{,}\) we see that \(4\) is the input to the inverse function. Since the inverse swaps inputs and outputs, that means that \(4\) is the output to the original function. So, we want to solve \(f(x)=4\text{:}\)
    \begin{align*} f(x) \amp = 4\\ 3x-7 \amp = 4\\ 3x \amp = 11 \\ x \amp = \frac{11}{3} \end{align*}
    Therefore, our final answer is \(f^{-1}(4)=\frac{11}{3}\text{.}\)
  2. Since \(g(x)=\dfrac{x}{x+3}\) and we want to evaluate \(g^{-1}(-4)\text{,}\) we see that \(-4\) is the input to the inverse function. Since the inverse swaps inputs and outputs, that means that \(-4\) is the output to the original function. So, we want to solve \(g(x)=-4\text{:}\)
    \begin{align*} g(x) \amp = -4\\ \dfrac{x}{x+3} \amp = -4\\ x \amp = -4(x+3)\\ x \amp = -4x -12 \\ 5x \amp = -12\\ x \amp = \frac{-12}{5} \end{align*}
    Therefore, our final answer is \(g^{-1}(-4)=\frac{-12}{5}\text{.}\)
  3. Since \(h(x)=x^3+1\) and we want to evaluate \(h^{-1}(9)\text{,}\) we see that \(9\) is the input to the inverse function. Since the inverse swaps inputs and outputs, that means that \(9\) is the output to the original function. So, we want to solve \(h(x)=9\text{:}\)
    \begin{align*} h(x) \amp = 9\\ x^3+1 \amp = 9\\ x^3 \amp = 8\\ x \amp = \sqrt[3]{8} \end{align*}
    Since \(\sqrt[3]{8}=2\text{,}\) our final answer is \(h^{-1}(9)=2\text{.}\)

Checkpoint 4.1.4.

Suppose \(p(x)\) is given in the graph below:
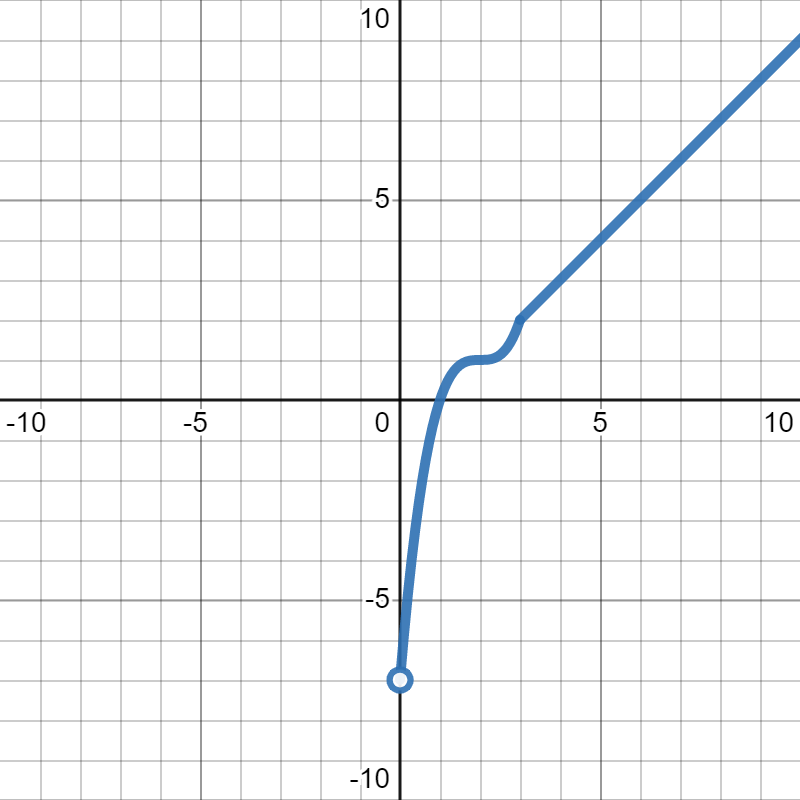
Evaluate \(p^{-1}(1)\text{.}\)
Answer.
\(p^{-1}(1)=2\)
Solution.
We want to find \(p^{-1}(1)\text{.}\) We can see that \(1\) is the input to the inverse function, which means its the output to the original function \(p(x)\text{.}\) That means we are looking for where \(y=1\text{.}\) Looking to the side, we see that the graph is at \((2,1)\text{,}\) which gives us our answer: \(p^{-1}(1)=2\text{.}\)

Checkpoint 4.1.5.

Suppose \(t(x)\) is given in the graph below:
Table 4.1.6.
\(x\) \(t(x)\)
\(-1\) \(2\)
\(0\) \(3\)
\(1.3\) \(-4\)
\(7\) \(0\)
\(14\) \(1\)
Find \(t^{-1}(0)\text{.}\)
Answer.
\(t^{-1}(0)=7\)
Solution.
We want to find \(t^{-1}(0)\text{.}\) We see that \(0\) is the input to the inverse, which means \(0\) is the output to the original function. So, we look for \(0\) in the second column of the table and find it in the fourth row of numbers. So, we look in the first column in the fourth row of numbers to get our answer: \(t^{-1}(0)=7\text{.}\)
PrevTopNext