Skip to main content

Exercises 7.3 Practice Problems

1.

Suppose \(f(x)=x^2-2\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=1\) to \(x=5\text{.}\)

Answer.
\(6\)

2.

Suppose \(f(x)\) is given in the graph below. Compute the average rate of change of \(f(x)\) from \(x=-5\) to \(x=2\text{.}\)

Answer.
\(1\)

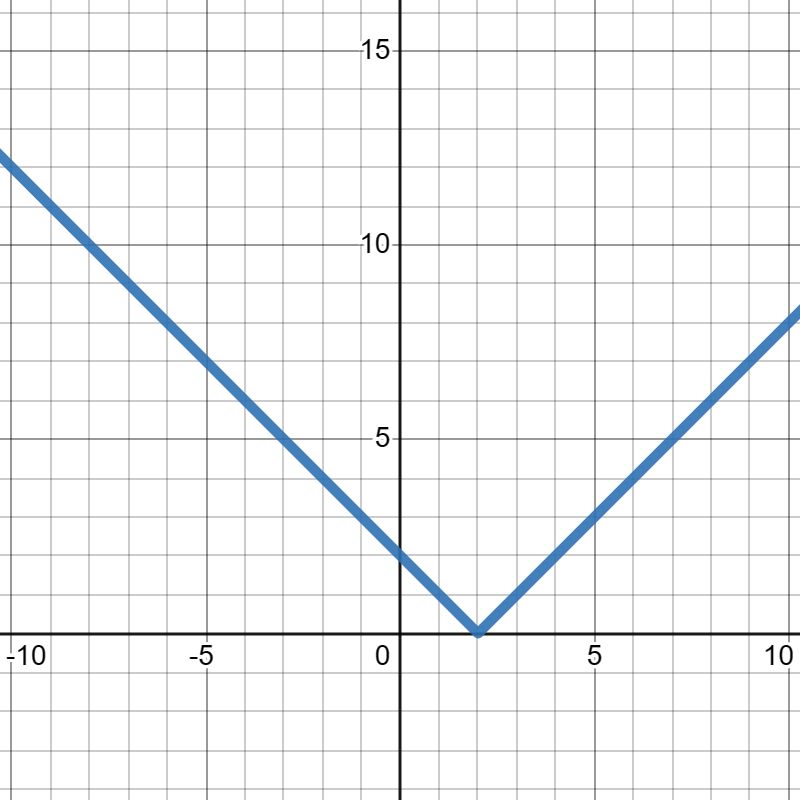
3.

Suppose \(f(x)=x^2 +2x +3\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=-1\) to \(x=1\text{.}\)

Answer.
\(2\)

4.

Suppose \(g(x)\) is given in the table below. Compute the average rate of change of \(g(x)\) from \(x=1\) to \(x=5\text{.}\)

Table 7.8.
\(x\) \(1\) \(2\) \(3\) \(4\) \(5\)
\(g(x)\) \(0\) \(2\) \(4\) \(1\) \(0\)
Answer.
\(0\)

5.

Suppose \(f(x)=\frac{x+3}{x-2}\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=0\) to \(x=4\text{.}\)

Answer.
\(\frac{5}{4}\)

6.

Suppose \(f(x)=x^3 + 5x\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=-2\) to \(x=2\text{.}\)

Answer.
\(9\)

7.

Suppose \(f(x)\) is given in the table below. Compute the average rate of change of \(f(x)\) from \(x=2\) to \(x=5\text{.}\)

Table 7.9.
\(x\) \(2\) \(4\) \(5\) \(7\) \(9\)
\(f(x)\) \(1\) \(-2\) \(4\) \(10\) \(0\)
Answer.
\(1\)

8.

Suppose \(f(x)=x^2+16\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=1\) to \(x=10\text{.}\)

Answer.
\(11\)

9.

Suppose \(g(x)\) is given in the table below. Compute the average rate of change of \(g(x)\) from \(x=1\) to \(x=7\text{.}\)

Table 7.10.
\(x\) \(1\) \(3\) \(5\) \(7\) \(15\)
\(g(x)\) \(10\) \(2\) \(14\) \(21\) \(0\)
Answer.
\(\frac{11}{6}\)

10.

Suppose \(f(x)=3x-7\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=-5\) to \(x=-2\text{.}\)

Answer.
\(3\)

11.

Suppose \(f(x)\) is given in the graph below. Compute the average rate of change of \(f(x)\) from \(x=0\) to \(x=4\text{.}\)

Answer.
\(1\)

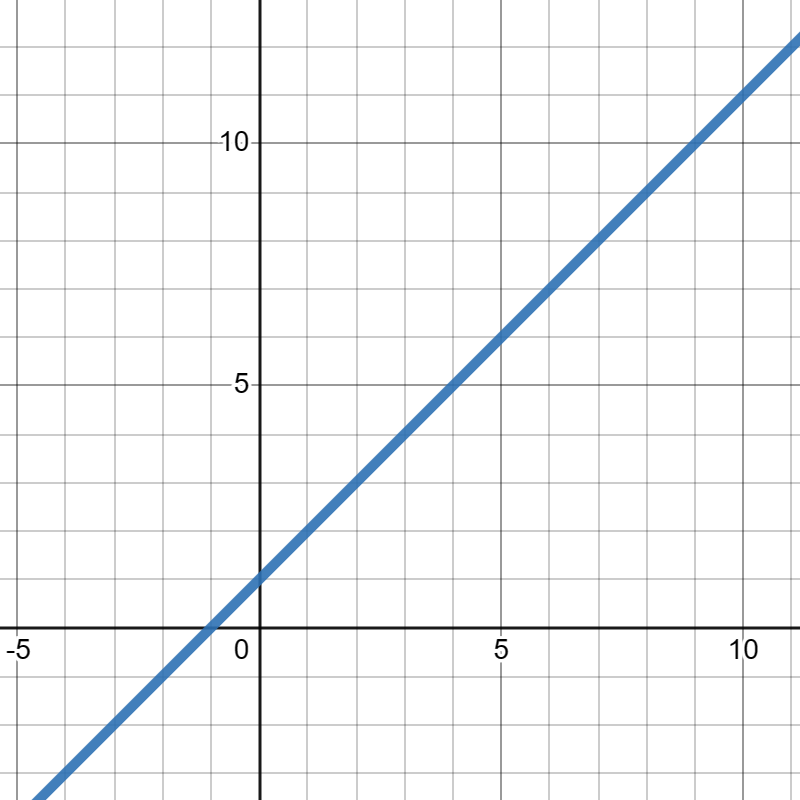
12.

Suppose \(f(x)=x^2-21\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=3\) to \(x=5\text{.}\)

Answer.
\(8\)

13.

Suppose \(f(x)=x^2-2\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=1\) to \(x=1+h\text{.}\)

Answer.
\(2+h\)

14.

Suppose \(f(x)=3x^2 +2x\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=2\) to \(x=2+h\text{.}\)

Answer.
\(3h+10\)

15.

Suppose \(f(x)=10x+2\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=a\) to \(x=a+h\text{.}\)

Answer.
\(10\)

16.

Suppose \(f(x)=x^2 +4x +4\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=a\) to \(x=a+h\text{.}\)

Answer.
\(h+2a+4\)

17.

Suppose \(f(x)=x^2+25\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=5\) to \(x=5+h\text{.}\)

Answer.
\(10+h\)

18.

Suppose \(f(x)=-x^2-3x+1\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=a\) to \(x=a+h\text{.}\)

Answer.
\(-2a-h+3\)

19.

Suppose \(f(x)=2x^2+10x\text{.}\) Compute the average rate of change of \(f(x)\) from \(x=3\) to \(x=3+h\text{.}\)

Answer.
\(2h+22\)