Section 9.3 Domain and Range of Transformations
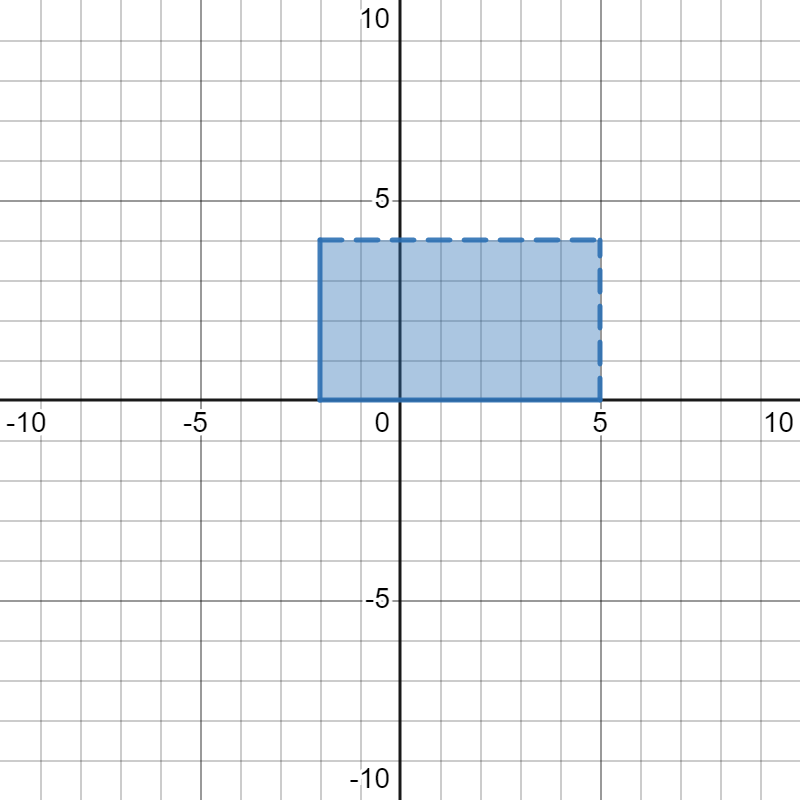
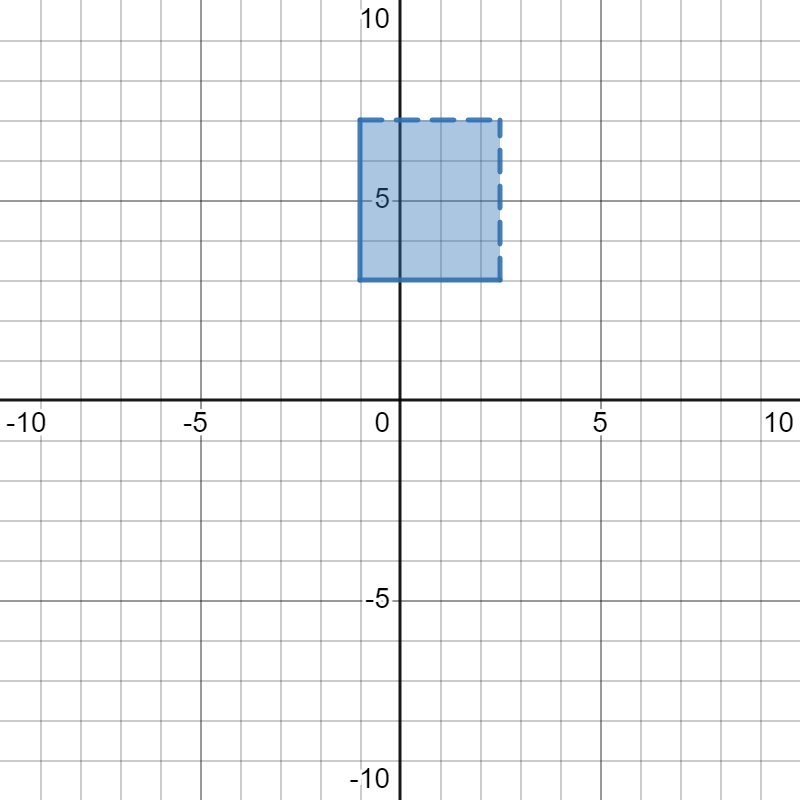
Fact 9.13. Domain and Range and Transformations.
| Direction | Transformation | Domain/Range | Conclusion |
|---|---|---|---|
| Vertical | Vertical transformations involve outputs (changes outside of the function) |
Range is about the outputs (y-values) that are covered |
Vertical transformations affect the range of a function |
| Horizontal | Horizontal transformations involve inputs (changes inside the function) |
Domain is about the inputs (x-values) that are covered |
Horizontal transformations affect the domain of a function |
Example 9.15.
Suppose we know that the domain of a function \(f(x)\) is \(\left(-2,5\right]\) and the range is \(\left[0,4\right)\text{.}\) We want to know the domain and range of the function \(g(x)=f(2x)+3\text{.}\)
The first thing we need to do is figure out what tranformations took \(f\) to \(g\text{.}\) Using what you learned in the previous sections, we can see that we have:
a vertical shift up by 3
a horizontal compression by 2
The vertical shift will move the whole graph up by 3, which means all of the y-values will increase by 3. So, the endpoints of the range will both increase by 3. Therefore, the range of \(g(x)\) is \(\left[3,7\right)\text{.}\)
The horizontal compression will squish all of the graph towards the y-axis by a factor of 2, which means all of the x-values will be cut in half. So, the endpoints of the domain will both be cut in half. Therefore, the domain of \(g(x)\) is \(\left(-1,\frac{5}{2}\right]\text{.}\)
You may find it helpful to draw a box to visualize the transformations. We don't know exactly what the graph looks like, but because we know the domain and range, it is somewhere in the box below:
After shifting it up by 3 and squishing towards the y-axis by 2, we end up with the following box, which gives us our new domain and range:
Checkpoint 9.16.
Suppose the domain of a function \(f(x)\) is \(\left[3,7\right)\) and its range is \(\left[-1,3\right]\text{.}\) What is the domain and range of the function \(g(x)=-f(x+2)\text{?}\)
The domain of \(g(x)\) is \(\left[1,5\right)\) and its range is \(\left[-3,1\right]\text{.}\)
The first thing we need to do is figure out what tranformations took \(f\) to \(g\text{.}\) Using what you learned in the previous sections, we can see that we have:
a vertical flip over the x-axis
a horizontal shift left by 2
The vertical flip will flip the entire graph over the x-axis, which means all of the y-values will change sign (negative becomes positive and positive becomes negative). So, the endpoints of the range will both change sign as well. Therefore, the range of \(g(x)\) is \(\left[-3,1\right]\text{.}\) Note that we still always write the lowest value first when writing interval notation.
The horizontal shift will move the entire graph to the left by 2, which means all of the x-values will go down by 2. So, the endpoints of the domain will also decrease by 2. Therefore, the domain of \(g(x)\) is \(\left[1,5\right)\text{.}\)