Suppose \(f(x)=x^2-7x\) and we want to evaluate \(3f(2)-4\text{.}\) Since we start with functions, we first need to find \(f(2)=(2)^2-7(2) = 4-14=-10\text{.}\) We can then plug that into our original expression and simplify: \(3(2)-4 = 3(-10)-4 = -34\text{.}\)
Section 2.4 Algebra with Functions
Example 2.4.1.
Checkpoint 2.4.2.
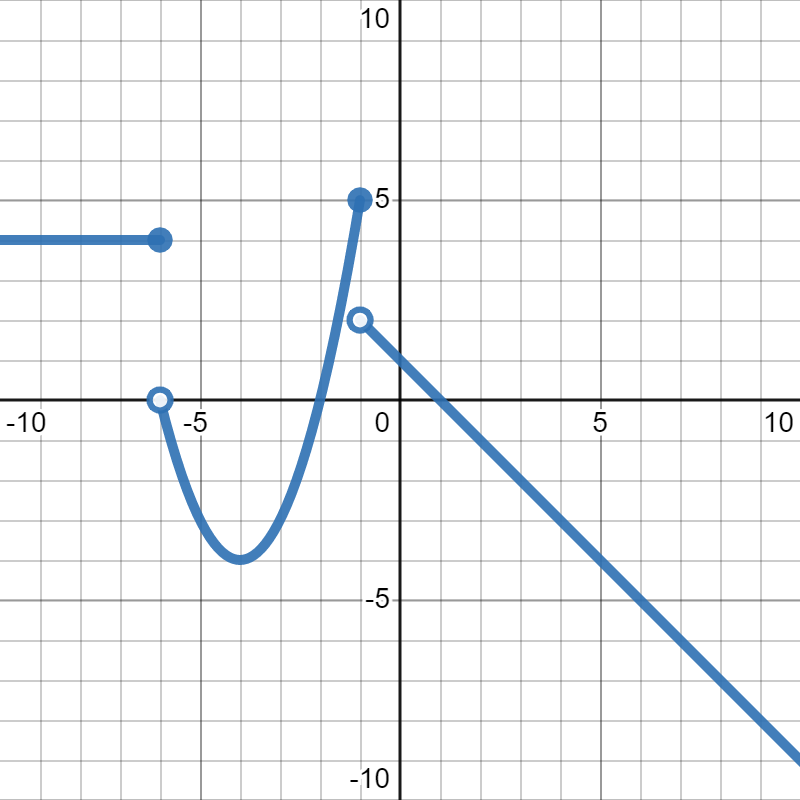
Evaluate \(7f(2)-(g(-2))^2+1\text{.}\)
Solution.
We start by evaluating the functions, but it doesn’t matter which function we start with. Let’s just go left-to-right:
\begin{equation*}
f(2)=3(2)-5 = 1
\end{equation*}
From the graph, we can see that \(g(-2)=0\text{.}\) So, we can plug those values into the original expression:
\begin{equation*}
7f(2)-(g(-2))^2+1 = 7(1)-(0)^2+1=8
\end{equation*}
Sometimes you’ll have some arithmetic to do inside your function before evaluating it. The key is to work from the inside out.
Example 2.4.3.
Suppose \(f(x)=x^2-8\) and we want to evaluate \(-f(2+3)+1\text{.}\) In that case, we start inside the function by simplifying \(2+3=5\text{.}\) Then, we can evaluate \(f(5)=(5)^2-8=17\text{.}\) Finally, we can plug that into our original expression to get the final answer:
\begin{equation*}
-f(2+3)+1 = -f(5)+1=-(17)+1=-16
\end{equation*}
