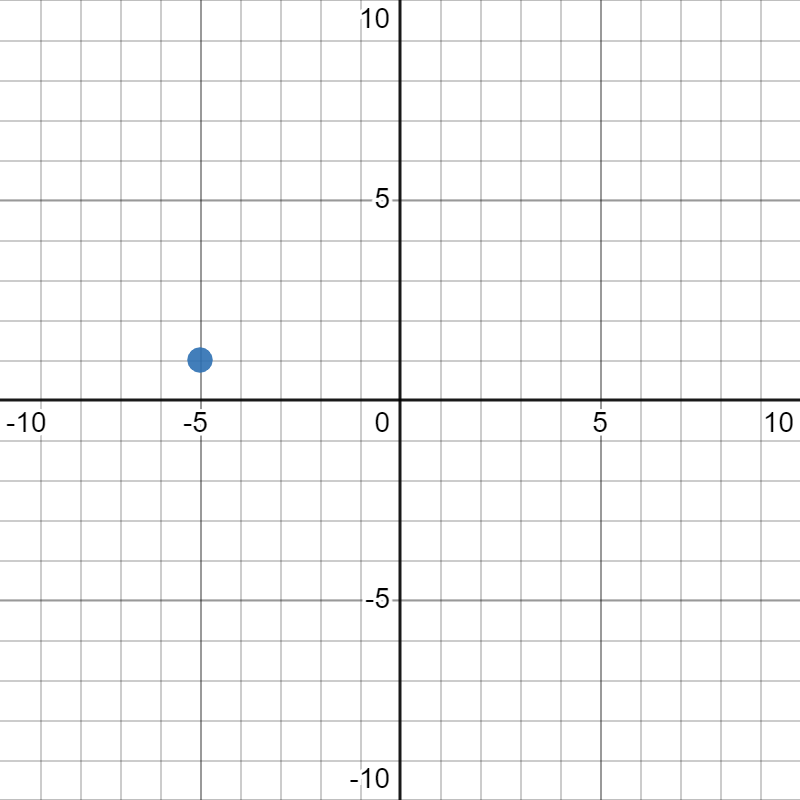
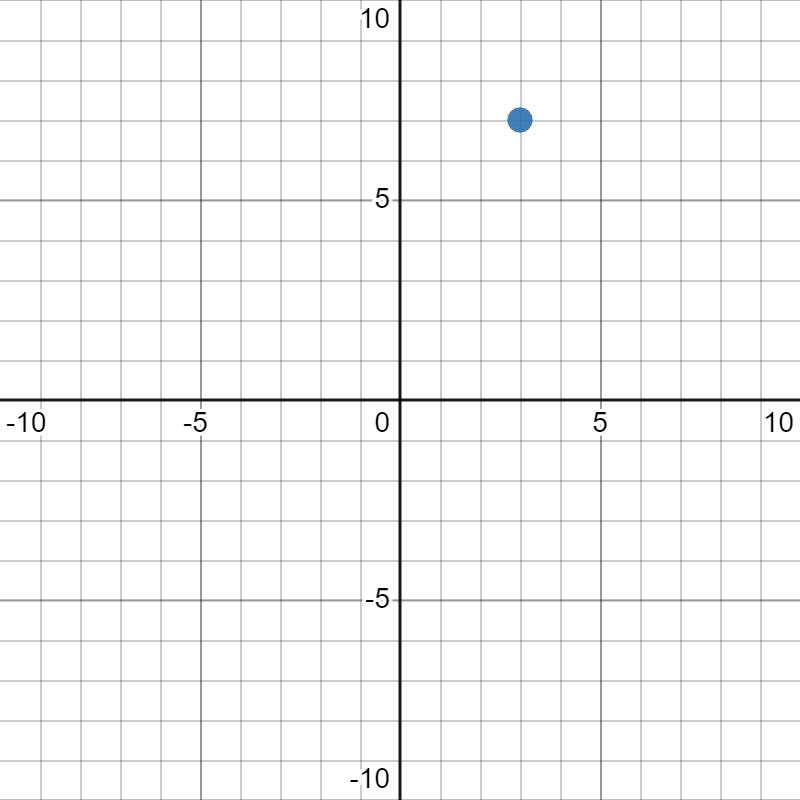
Suppose we want to figure out the coordinates of the point plotted below:
To figure out the
\(x\)-coordiante, we trace up/down to the
\(x\)-axis to see what number we land at. In this case, we trace down and see that we are at
\(-5\text{,}\) so that is our
\(x\)-coordinate. To figure out the
\(y\)-coordiante, we trace left/right to the
\(y\)-axis to see what number we land at. In this case, we trace to the right and see that we are at
\(1\text{,}\) so that is our
\(y\)-coordinate. Now that we have both coordinates, we can put it all together for our final answer:
\((-5,1)\text{.}\)