Skip to main content

Exercises 3.3 Practice Problems

1.

Suppose \(f(x) = (x+2)^2 \) and \(g(x)\) is given in the graph below:

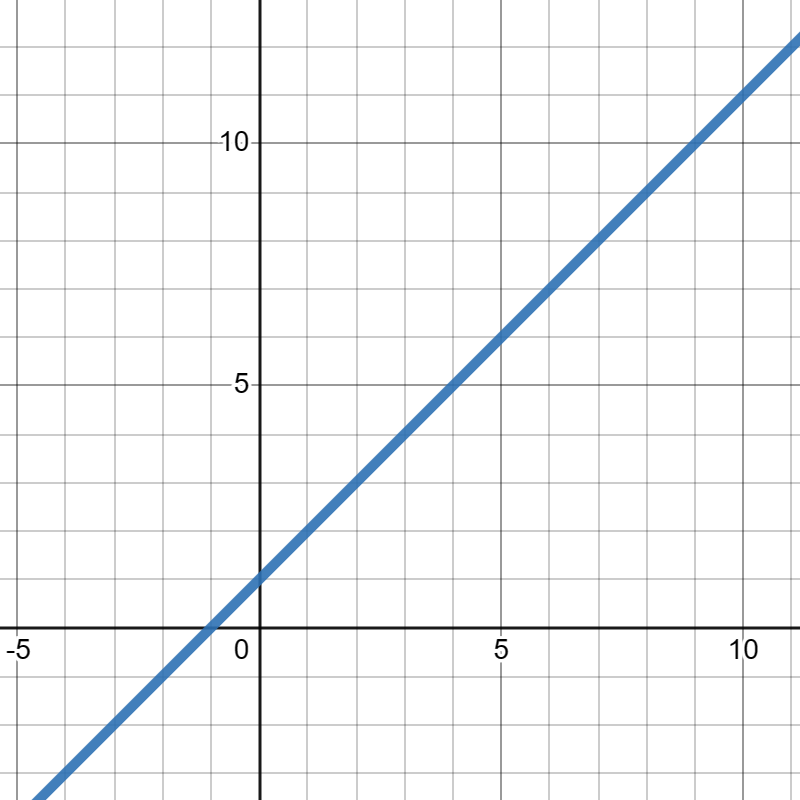
Evaluate each of the following:

  1. \(\displaystyle f(g(-2))\)

  2. \(\displaystyle f(g(4))\)

  3. \(\displaystyle g(g(6))\)

  4. \(\displaystyle g(f(0))\)

  5. \(\displaystyle f(g(0))\)

Answer.

  1. \(\displaystyle f(g(-2))=1\)

  2. \(\displaystyle f(g(4))=49\)

  3. \(\displaystyle g(g(6))=8\)

  4. \(\displaystyle g(f(0))=5\)

  5. \(\displaystyle f(g(0))=9\)

2.

Suppose \(f(x) = \frac{1}{2}x \) and \(g(x)\) is given in the table below:

Table 3.8.
\(x\) \(-1\) \(1\) \(2\) \(5\) \(4\)
\(g(x)\) \(0\) \(2\) \(4\) \(1\) \(0\)

Evaluate each of the following:

  1. \(\displaystyle f(g(-1))\)

  2. \(\displaystyle f(g(5))\)

  3. \(\displaystyle g(g(2))\)

  4. \(\displaystyle g(f(-2))\)

  5. \(\displaystyle f(g(1))\)

Answer.

  1. \(\displaystyle f(g(-1))=0\)

  2. \(\displaystyle f(g(5))=\frac{1}{2}\)

  3. \(\displaystyle g(g(2))=0\)

  4. \(\displaystyle g(f(-2))=0\)

  5. \(\displaystyle f(g(1))=1\)

3.

Suppose \(f(x)\) is given in the graph below and \(g(x)\) is given in the table below:

Table 3.9.
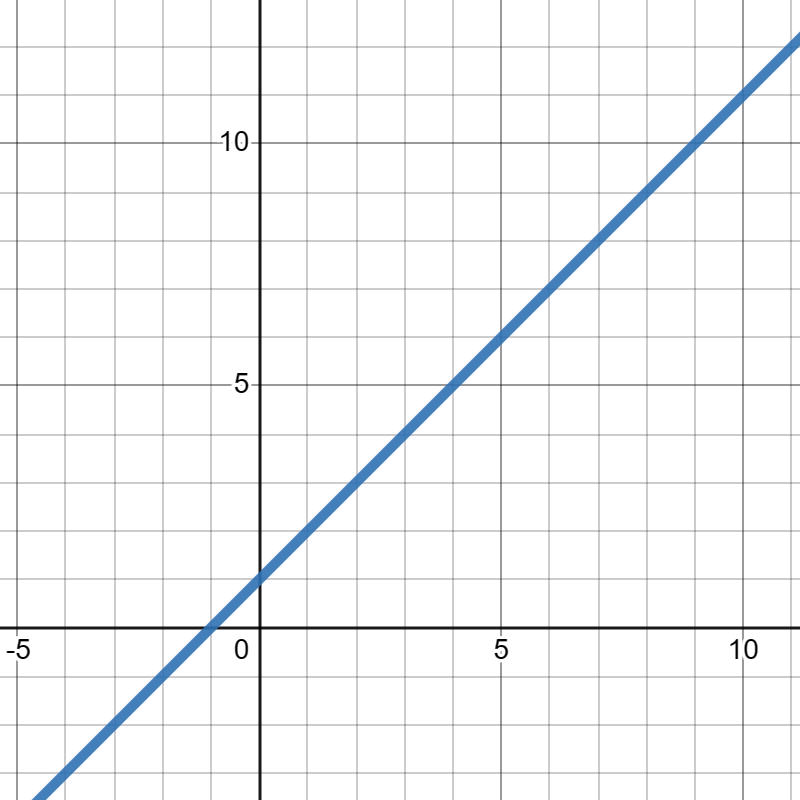
\(x\) \(1\) \(2\) \(3\) \(4\) \(5\)
\(g(x)\) \(0\) \(2\) \(4\) \(1\) \(5\)

Evaluate each of the following or, if there is insufficient information given to answer the question, state that.

  1. \(\displaystyle f(g(1))\)

  2. \(\displaystyle f(g(5))\)

  3. \(\displaystyle g(g(2))\)

  4. \(\displaystyle g(f(-2))\)

  5. \(\displaystyle f(g(1))\)

Answer.

  1. \(\displaystyle f(g(1))=5\)

  2. \(\displaystyle f(g(5))=0\)

  3. \(\displaystyle g(g(2))=2\)

  4. There is insuffient information given to compute.

  5. \(\displaystyle f(g(3))=1\)

4.

Suppose \(g(x)\) is given in the graph below and \(h(x)\) is given in the table below:

Table 3.10.
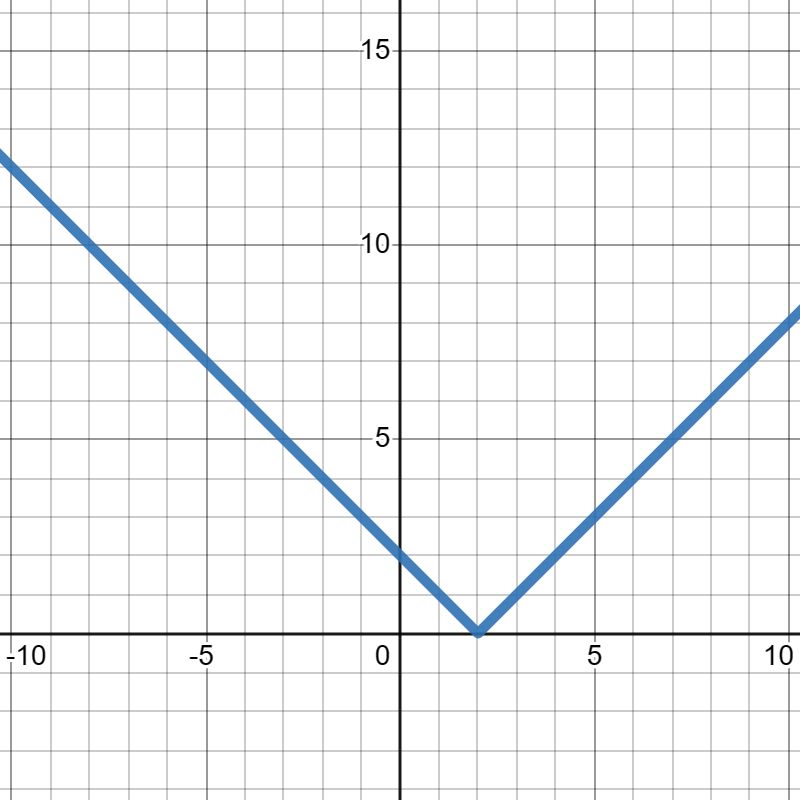
\(x\) \(0\) \(2\) \(4\) \(6\) \(8\)
\(h(x)\) \(0\) \(8\) \(4\) \(6\) \(2\)

Evaluate each of the following or, if there is insufficient information given to answer the question, state that.

  1. \(\displaystyle h(g(1))\)

  2. \(\displaystyle h(g(4))\)

  3. \(\displaystyle h(g(2))\)

  4. \(\displaystyle g(h(2))\)

  5. \(\displaystyle h(h(2))\)

Answer.

  1. There is insuffient information given to compute.

  2. \(\displaystyle h(g(4))=8\)

  3. \(\displaystyle h(g(2))=0\)

  4. \(\displaystyle g(h(2))=0\)

  5. \(\displaystyle h(h(2))=2\)

5.

Suppose \(g(x)=x^2\) and \(h(x)=|x+1|\) is given in the table below:

Evaluate each of the following or, if there is insufficient information given to answer the question, state that.

  1. \(\displaystyle h(g(1))\)

  2. \(\displaystyle h(g(2))\)

  3. \(\displaystyle h(g(-1))\)

  4. \(\displaystyle g(h(-1))\)

  5. \(\displaystyle h(h(-1))\)

Answer.

  1. \(\displaystyle h(g(1))=2\)

  2. \(\displaystyle h(g(2))=5\)

  3. \(\displaystyle h(g(-1))=2\)

  4. \(\displaystyle g(h(-1))=0\)

  5. \(\displaystyle h(h(-1))=1\)

6.

Suppose \(f(x)=2x+3\) and \(g(x)=x^2+x-1\text{.}\) Find each of the following. You do NOT need to simplify.

  1. \(\displaystyle f(g(x))\)

  2. \(\displaystyle g(f(x))\)

  3. \(\displaystyle f(f(x))\)

  4. \(\displaystyle g(g(x))\)

Answer.

  1. \(\displaystyle f(g(x))=2(x^2+x-1)+3\)

  2. \(\displaystyle g(f(x))=(2x+3)^2+(2x+3)-1\)

  3. \(\displaystyle f(f(x))=2(2x+3)+3\)

  4. \(\displaystyle g(g(x))=(x^2+x-1)^2+(x^2+x-1)-1\)

7.

Suppose \(f(x)=|x+3|\) and \(g(x)=3x-1\text{.}\) Find each of the following. You do NOT need to simplify.

  1. \(\displaystyle f(g(x))\)

  2. \(\displaystyle g(f(x))\)

  3. \(\displaystyle f(f(x))\)

  4. \(\displaystyle g(g(x))\)

Answer.

  1. \(\displaystyle f(g(x))=|(3x-1)+3|\)

  2. \(\displaystyle g(f(x))=3|x+3|-1\)

  3. \(\displaystyle f(f(x))=||x+3|+3|\)

  4. \(\displaystyle g(g(x))=3(3x-1)-1\)

8.

Suppose \(f(x)=\frac{1}{2}x+1\) and \(g(x)=\frac{x+1}{2}\text{.}\) Find each of the following. You do NOT need to simplify.

  1. \(\displaystyle f(g(x))\)

  2. \(\displaystyle g(f(x))\)

  3. \(\displaystyle f(f(x))\)

  4. \(\displaystyle g(g(x))\)

Answer.

  1. \(\displaystyle f(g(x))=\frac{1}{2}\left(\frac{x+1}{2}\right)+1\)

  2. \(\displaystyle g(f(x))=\frac{\left(\frac{1}{2}x+1\right)+1}{2}\)

  3. \(\displaystyle f(f(x))=\frac{1}{2}\left(\frac{1}{2}x+1\right)+1\)

  4. \(\displaystyle g(g(x))=\frac{\left(\frac{x+1}{2}\right)+1}{2}\)

9.

Suppose \(f(x)=\sqrt{x}\) and \(g(x)=4x+5\text{.}\) Find each of the following. You do NOT need to simplify.

  1. \(\displaystyle f(g(x))\)

  2. \(\displaystyle g(f(x))\)

  3. \(\displaystyle f(f(x))\)

  4. \(\displaystyle g(g(x))\)

Answer.

  1. \(\displaystyle f(g(x))=\sqrt{4x+5}\)

  2. \(\displaystyle g(f(x))=4\sqrt{x}+5\)

  3. \(\displaystyle f(f(x))=\sqrt{\sqrt{x}}\)

  4. \(\displaystyle g(g(x))=4(4x+5)+5\)