Skip to main content

Exercises 4.3 Practice Problems

1.

Suppose \(f(x) = 2x+1\text{.}\)

Evaluate each of the following:

  1. \(\displaystyle f^{-1}(0)\)

  2. \(\displaystyle f^{-1}(4)\)

  3. \(\displaystyle f^{-1}(9)\)

  4. \(\displaystyle f^{-1}(1)\)

  5. \(\displaystyle f^{-1}(10)\)

Answer.

  1. \(\displaystyle f^{-1}(0)=\frac{-1}{2}\)

  2. \(\displaystyle f^{-1}(4)=\frac{3}{2}\)

  3. \(\displaystyle f^{-1}(9)=4\)

  4. \(\displaystyle f^{-1}(1)=0\)

  5. \(\displaystyle f^{-1}(10)=\frac{9}{2}\)

2.

Suppose \(f(x) = 3x-2\text{.}\)

Evaluate each of the following:

  1. \(\displaystyle f^{-1}(1)\)

  2. \(\displaystyle f^{-1}(3)\)

  3. \(\displaystyle f^{-1}(0)\)

  4. \(\displaystyle f^{-1}(5)\)

  5. \(\displaystyle f^{-1}(4)\)

Answer.

  1. \(\displaystyle f^{-1}(1)=1\)

  2. \(\displaystyle f^{-1}(3)=\frac{5}{3}\)

  3. \(\displaystyle f^{-1}(0)=\frac{2}{3}\)

  4. \(\displaystyle f^{-1}(5)=\frac{7}{3}\)

  5. \(\displaystyle f^{-1}(4)=2\)

3.

Suppose \(f(x)\) is given in the graph below.

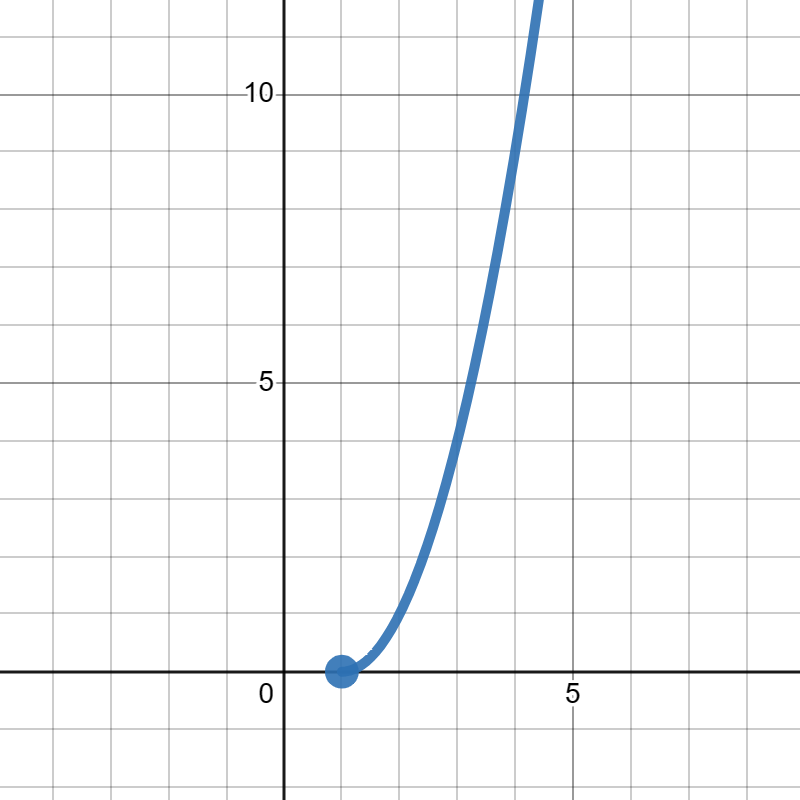
Evaluate each of the following:

  1. \(\displaystyle f^{-1}(0)\)

  2. \(\displaystyle f^{-1}(1)\)

  3. \(\displaystyle f^{-1}(9)\)

  4. \(\displaystyle f^{-1}(2)\)

  5. \(\displaystyle f^{-1}(4)\)

Answer.

  1. \(\displaystyle f^{-1}(0)=1\)

  2. \(\displaystyle f^{-1}(1)=2\)

  3. \(\displaystyle f^{-1}(9)=5\)

  4. \(\displaystyle f^{-1}(2)=3\)

  5. \(\displaystyle f^{-1}(4)=4\)

4.

Suppose \(g(x)\) is given in the table below.

Table 4.11.
\(x\) \(-1\) \(3\) \(2\) \(5\) \(4\)
\(g(x)\) \(0\) \(3\) \(7\) \(1\) \(2\)

Evaluate each of the following:

  1. \(\displaystyle g^{-1}(0)\)

  2. \(\displaystyle g^{-1}(1)\)

  3. \(\displaystyle g^{-1}(3)\)

  4. \(\displaystyle g^{-1}(7)\)

  5. \(\displaystyle g^{-1}(2)\)

Answer.

  1. \(\displaystyle g^{-1}(0)=-1\)

  2. \(\displaystyle g^{-1}(1)=5\)

  3. \(\displaystyle g^{-1}(3)=3\)

  4. \(\displaystyle g^{-1}(7)=2\)

  5. \(\displaystyle g^{-1}(2)=4\)

5.

Suppose \(g(x)\) is given in the table below.

Table 4.12.
\(x\) \(0\) \(2\) \(3\) \(5\) \(4\)
\(g(x)\) \(0\) \(1\) \(7\) \(5\) \(2\)

Evaluate each of the following:

  1. \(\displaystyle g^{-1}(0)\)

  2. \(\displaystyle g^{-1}(1)\)

  3. \(\displaystyle g^{-1}(2)\)

  4. \(\displaystyle g^{-1}(7)\)

  5. \(\displaystyle g^{-1}(5)\)

Answer.

  1. \(\displaystyle g^{-1}(0)=0\)

  2. \(\displaystyle g^{-1}(1)=2\)

  3. \(\displaystyle g^{-1}(2)=4\)

  4. \(\displaystyle g^{-1}(7)=3\)

  5. \(\displaystyle g^{-1}(5)=5\)

6.

Suppose \(f(x) = 5x+7.\)

Find a formula for the inverse.

Answer.

\(f^{-1}(x)=\frac{x-7}{5}\)

7.

Suppose \(g(x) = \frac{x+3}{2x-4}\text{.}\)

Find a formula for the inverse.

Answer.

\(g^{-1}(x)=\frac{3+4x}{2x-1}\)

8.

Suppose \(f(x) = x^3 -3\text{.}\)

Find a formula for the inverse.

Answer.

\(f^{-1}(x)=\sqrt[3]{x+3}\)

9.

Suppose \(g(x) = \frac{2x+3}{5x-4}\text{.}\)

Find a formula for the inverse.

Answer.

\(g^{-1}(x)=\frac{3+4x}{5x-2}\)

10.

Suppose \(g(x) = (x+1)^5\text{.}\)

Find a formula for the inverse.

Answer.

\(g^{-1}(x)=\sqrt[5]{x}-1 \)

11.

Suppose \(g(x) = \frac{2}{7x-3}\text{.}\)

Find a formula for the inverse.

Answer.

\(g^{-1}(x)=\frac{2+3x}{7x}\)

12.

Suppose \(g(x) = \sqrt[7](x) + 8\text{.}\)

Find a formula for the inverse.

Answer.

\(g^{-1}(x)= (x-8)^{7}\)