Intercepts

Section 1.2 Intercepts

Definition 1.2.0.7.

The \(x\)-intercepts of a graph are the points where it touches the \(x\)-axis. The \(y\)-intercepts of a graph are the points where it touches the \(y\)-axis.In this class, we will always write the intercepts as ordered pairs.

🔗

Example 1.2.0.8.

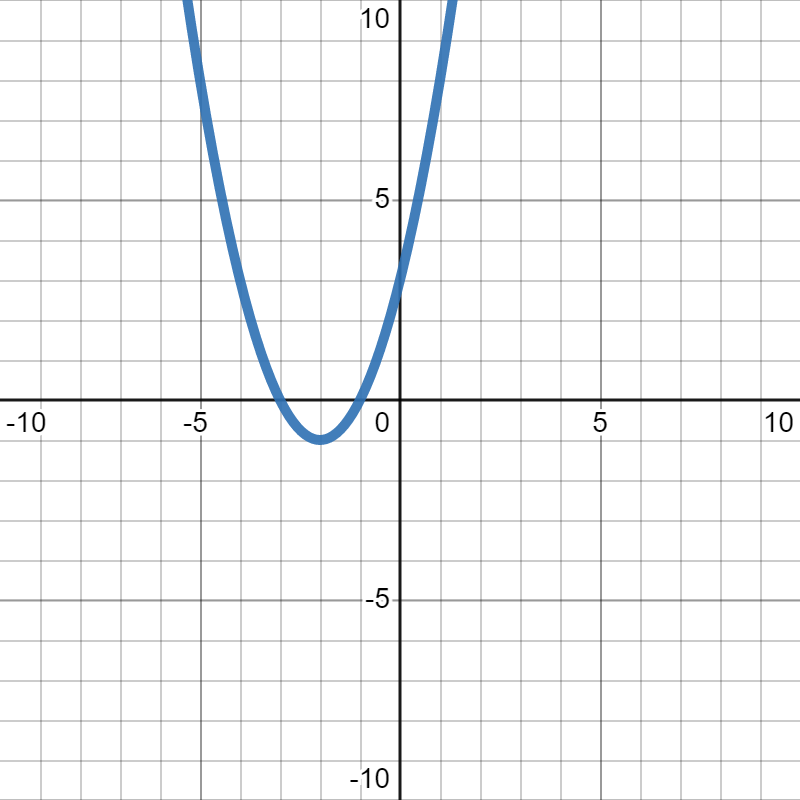
Suppose we want to find the \(x\)- and \(y\)-intercepts of the graph below:

🔗

Looking along the \(x\)-axis, we see that the graph crosses it where \(x=-3\) and where \(x=-1\text{.}\) Since we need to write them as ordered pairs, and any point on the \(x\)-axis has \(y=0\text{,}\) that means we have two \(x\)-intercepts: \((-3,0)\) and \((-1,0)\text{.}\)

🔗

Looking along the \(y\)-axis, we see that the graph crosses it where \(y=3\text{.}\) Since we need to write them as ordered pairs, and any point on the \(y\)-axis has \(x=0\text{,}\) that means we have the \(y\)-intercept at \((0,3)\text{.}\)

🔗

In the last example, we could see that the \(y\)-intercept is at \(y=3\) because that is about where it looks like the graph crosses, and in this class, numbers from graphs will be nice numbers. But in reality, the graph just isn’t detailed enough for us to be able to tell if it’s really at \(y=3\) or if it’s really at \(y=3.1\) or at \(y=2.97\text{.}\) If we have a formula that defines the graph, we can use algebra to figure out exactly what the intercepts are.

🔗

Fact 1.2.0.9.

Since the \(x\)-intercepts are where the graph crosses the \(x\)-axis, and every point there has \(y=0\text{,}\) to find \(x\)-intercepts algebraically, plug \(y=0\) into the equation and solve for \(x\).

🔗
Since the \(y\)-intercepts are where the graph crosses the \(y\)-axis, and every point there has \(x=0\text{,}\) to find \(y\)-intercepts algebraically, plug \(x=0\) into the equation and solve for \(y\).

🔗

🔗

Example 1.2.0.10.

Suppose we want to find the \(x\)- and \(y\)-intercepts of \(y=x^2-5\text{.}\)

🔗

Let’s start with the \(x\)-intercepts. We need to plug in \(y=0\) and solve for \(x\text{.}\)

🔗

\begin{align*} 0\amp=x^2-5\\ 5\amp=x^2\\ \pm \sqrt{5}\amp=x \end{align*}

Therefore, our \(x\)-intercepts are \((\sqrt{5},0)\) and \((-\sqrt{5},0)\text{.}\)

🔗

Now, let’s find the \(y\)-intercepts. We need to plug in \(x=0\) and solve for \(y\text{.}\)

🔗

\begin{equation*} y=(0)^2-5=-5 \end{equation*}

Therefore, our \(y\)-intercept is \((0,-5)\text{.}\)

🔗

Throughout this class, we will look at many different functions, and some will have shortcuts for finding one kind of intercept or the other. However, the strategy shown here will always work. It’s a very powerful tool that you’ll want to remember, because we’ll use it all semester long.

🔗