Exercises 9.4 Practice Problems
1.
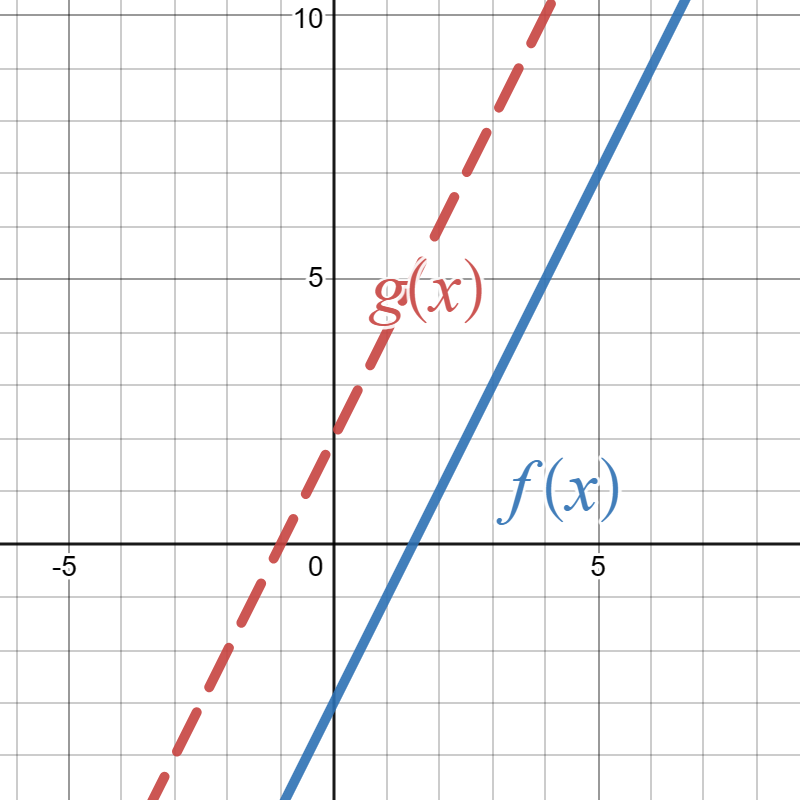
Below is the graph of \(f(x)\text{.}\)
2.
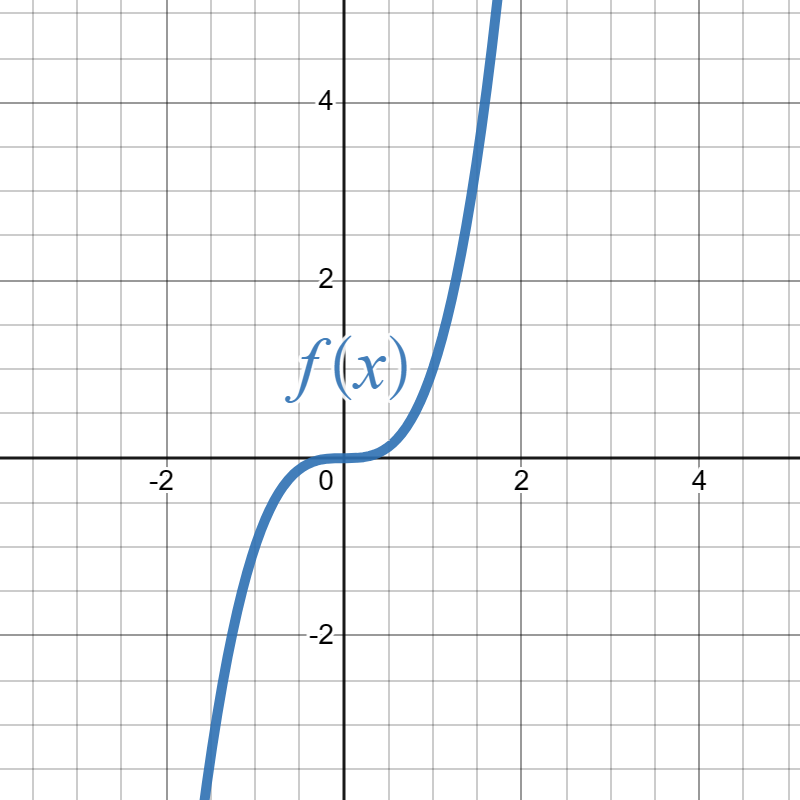
Below is the graph of \(f(x)\text{.}\)
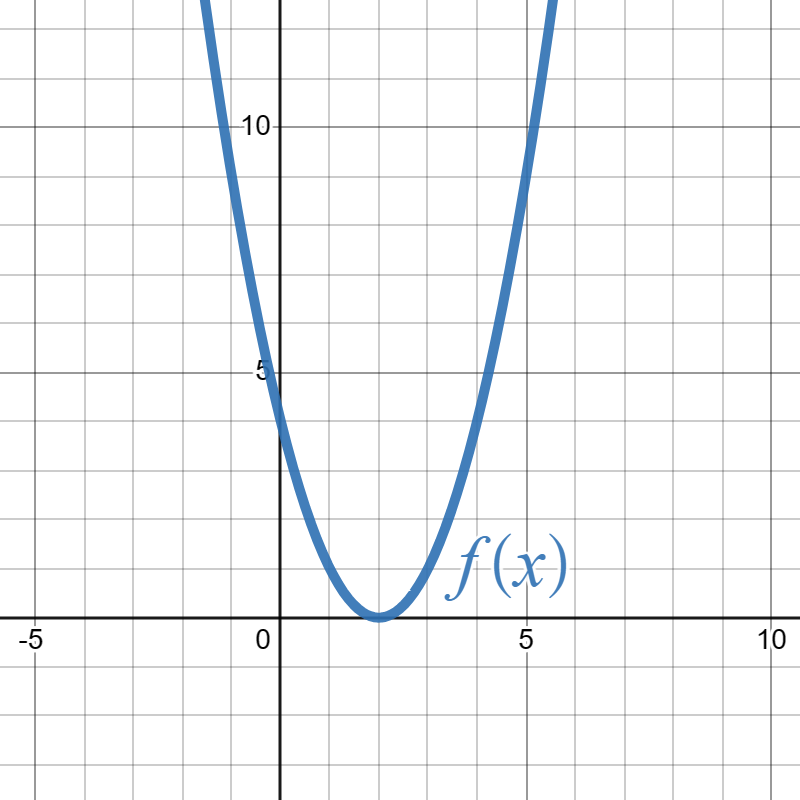
3.
Below is the graph of \(f(x)\text{.}\)
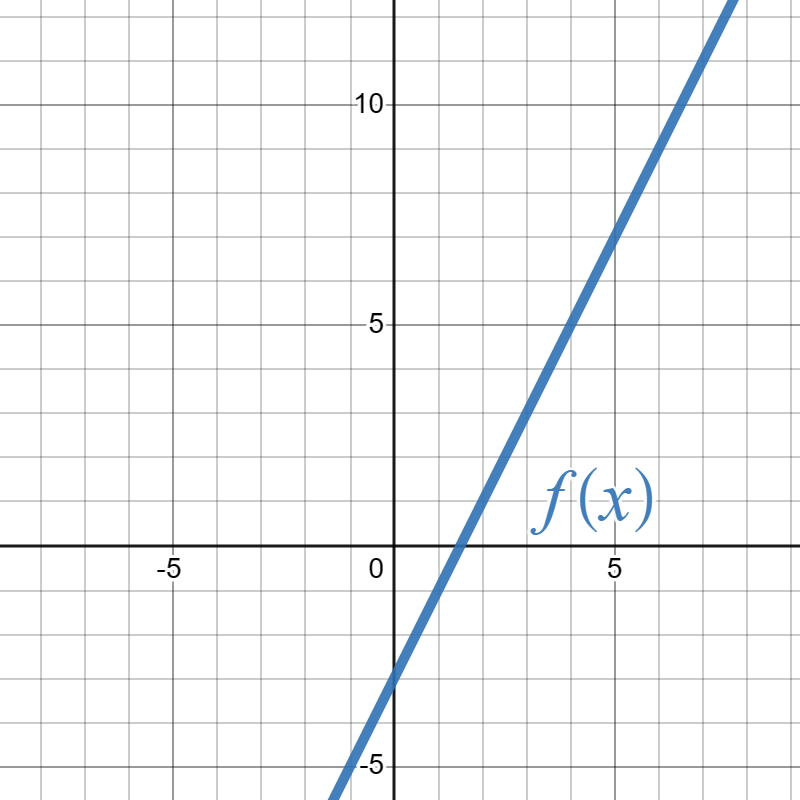
4.
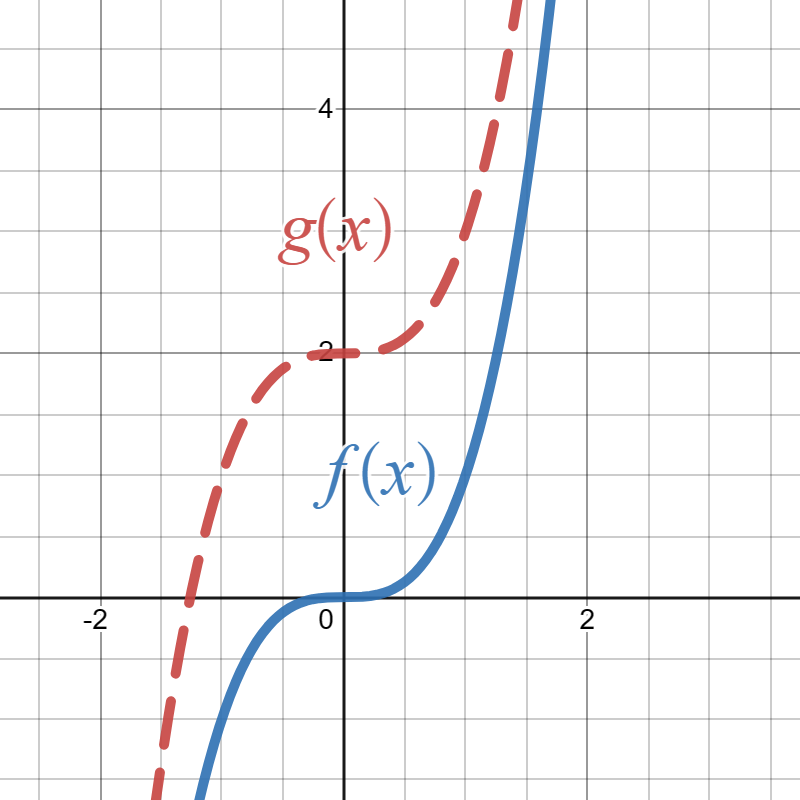
Suppose the solid blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
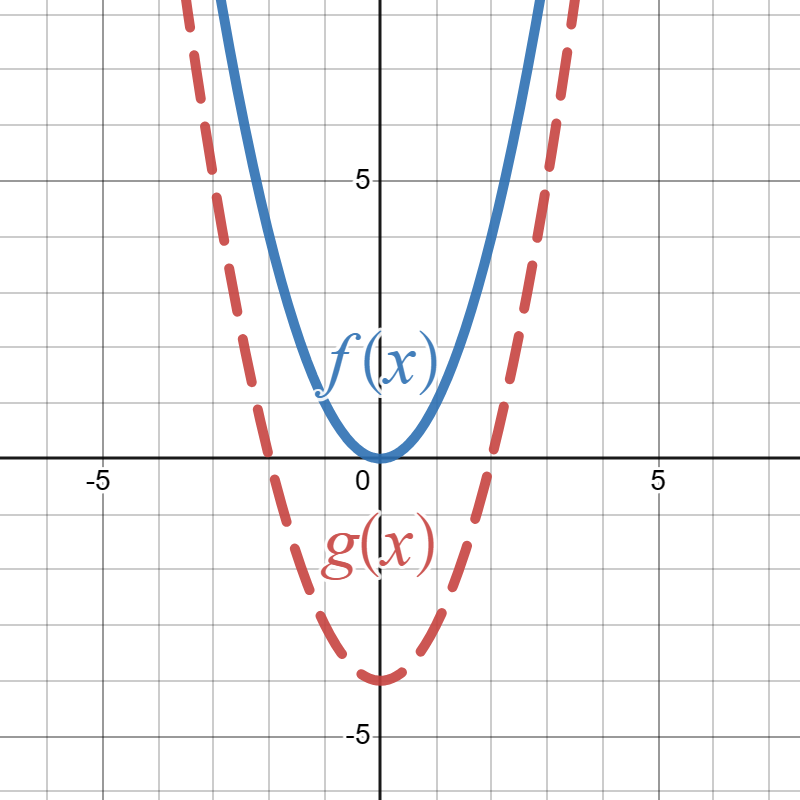
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f(x)-4\)
5.
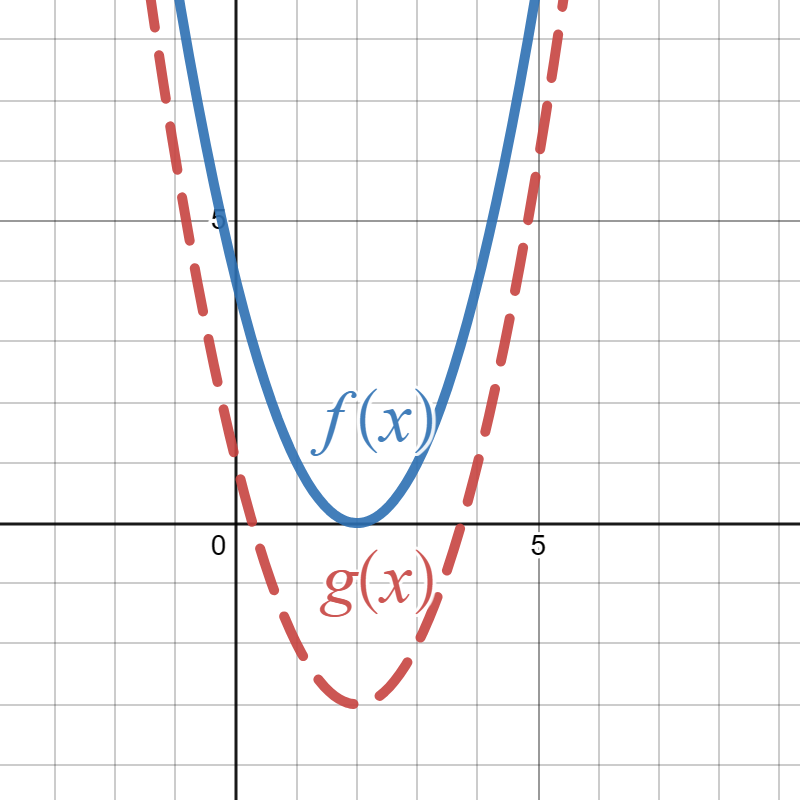
Suppose the solid blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
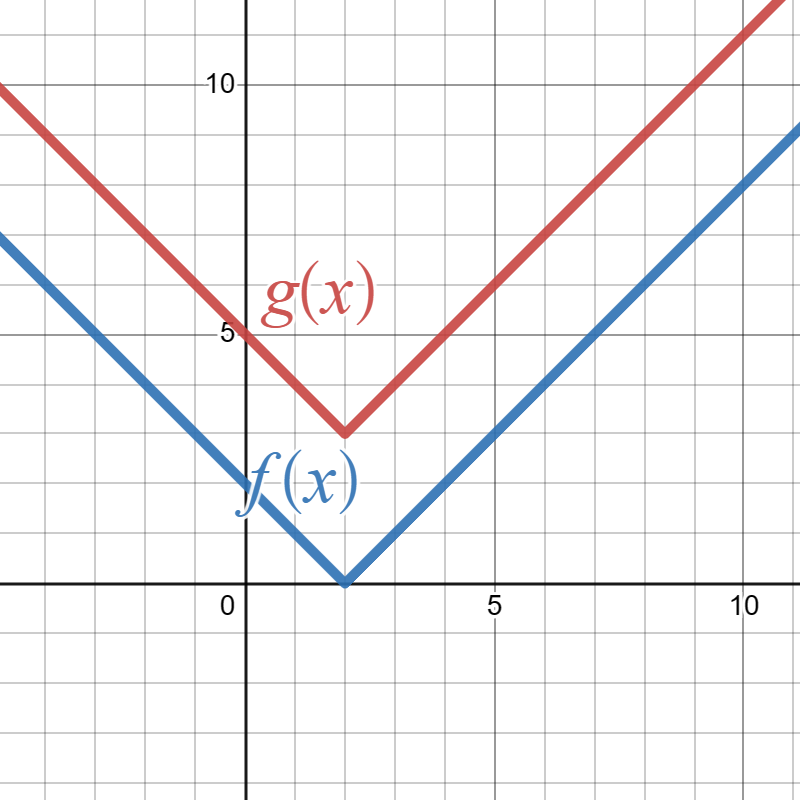
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f(x)+3\)
6.
Suppose \(f(x)=x^3-2x+1\) and \(g(x)\) is the same as \(f(x)\) but shifted down by \(3\text{.}\) Write a formula for \(g(x)\text{.}\)
\(g(x)=x^3-2x-2\)
7.
Suppose \(f(x)=3x^2\) and \(g(x)=3x^2-4\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
Shift down by \(4\text{.}\)
8.
Suppose \(f(x)=x^2-3\) and \(g(x)\) is the same as \(f(x)\) but shifted up by \(1\text{.}\) Write a formula for \(g(x)\text{.}\)
\(g(x)=x^2-2\)
9.
Suppose \(f(x)=3x+4\) and \(g(x)=3x+8\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
Shift up by \(4\text{.}\)
10.
Suppose the domain of a function \(f(x)\) is \(\left[1,5\right)\) and its range is \(\left[-1,4\right]\text{.}\) What is the domain and range of the function \(g(x)=f(x+2)-3\text{?}\)
The domain of \(g(x)\) is \(\left[-1,3\right)\) and its range is \(\left[-4,1\right]\text{.}\)
11.
Suppose the domain of a function \(f(x)\) is \(\left[0,10\right)\) and its range is \(\left[-10,2\right]\text{.}\) What is the domain and range of the function \(g(x)=-2f(x)\text{?}\)
The domain of \(g(x)\) is \(\left[0,10\right)\) and its range is \(\left[-4,20\right]\text{.}\)
12.
Suppose the domain of a function \(f(x)\) is \(\left[-2,7\right)\) and its range is \(\left[0,8\right]\text{.}\) What is the domain and range of the function \(g(x)=f(-x)+1\text{?}\)
The domain of \(g(x)\) is \(\left(-7,2\right]\) and its range is \(\left[1,9\right]\text{.}\)
13.
Suppose the domain of a function \(f(x)\) is \(\left[-7,8\right)\) and its range is \(\left[3,12\right]\text{.}\) What is the domain and range of the function \(g(x)=f(2x)-1\text{?}\)
The domain of \(g(x)\) is \(\left[-\frac{7}{2},4\right)\) and its range is \(\left[2,11\right]\text{.}\)
14.
Suppose \(g(x)=2f(x-3)\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical stretch by 2 and a horizontal shift right by 3.
15.
Suppose \(g(x)=f(-x)+2\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a horizontal flip and a vertical shift up by 2.
16.
Suppose \(g(x)=-f(x+1)\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical flip and a horizontal shift left by 1.
17.
Suppose \(g(x)=f(\frac{1}{2}x)-4\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a horizontal stretch by 2 and a vertical shift down by 4.
18.
Suppose \(g(x)=f(x-8)+6\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical shift up by 6 and a horizontal shift right by 8.
19.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
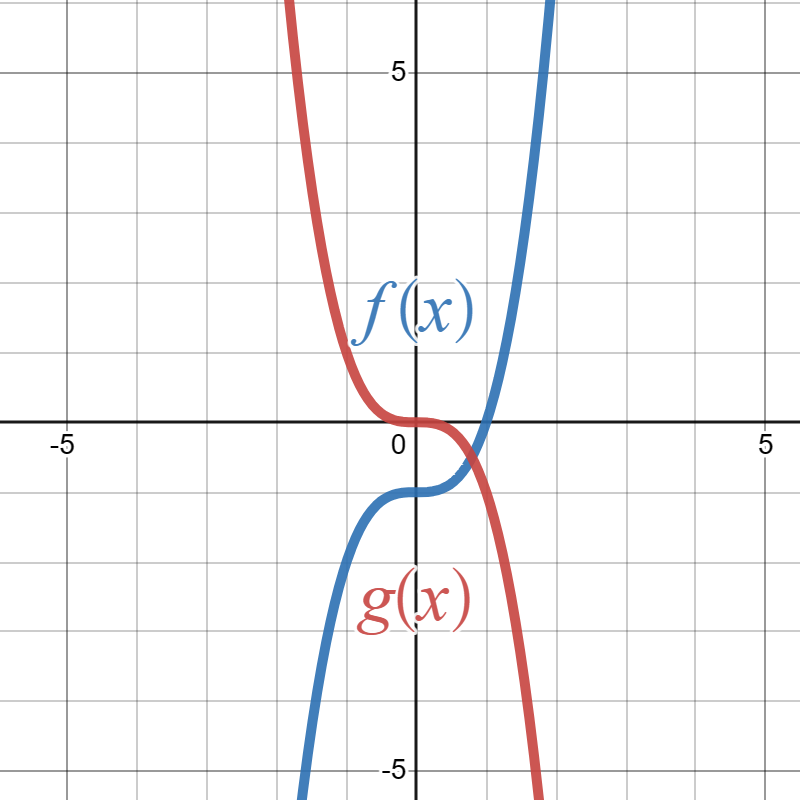
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f\left(-x\right)+1\)
20.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
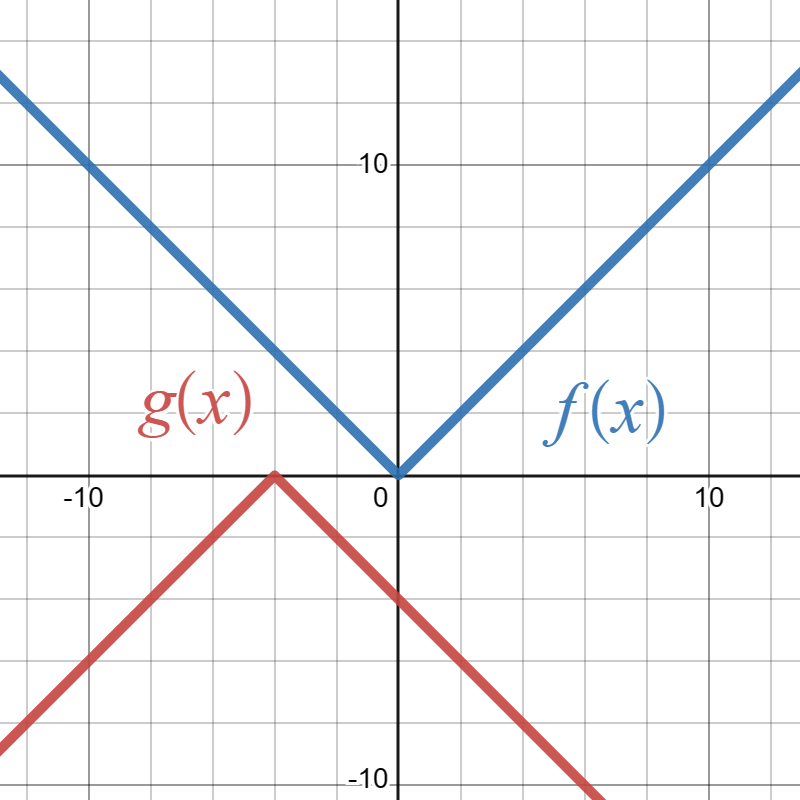
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=-f\left(x+4\right)\)
21.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
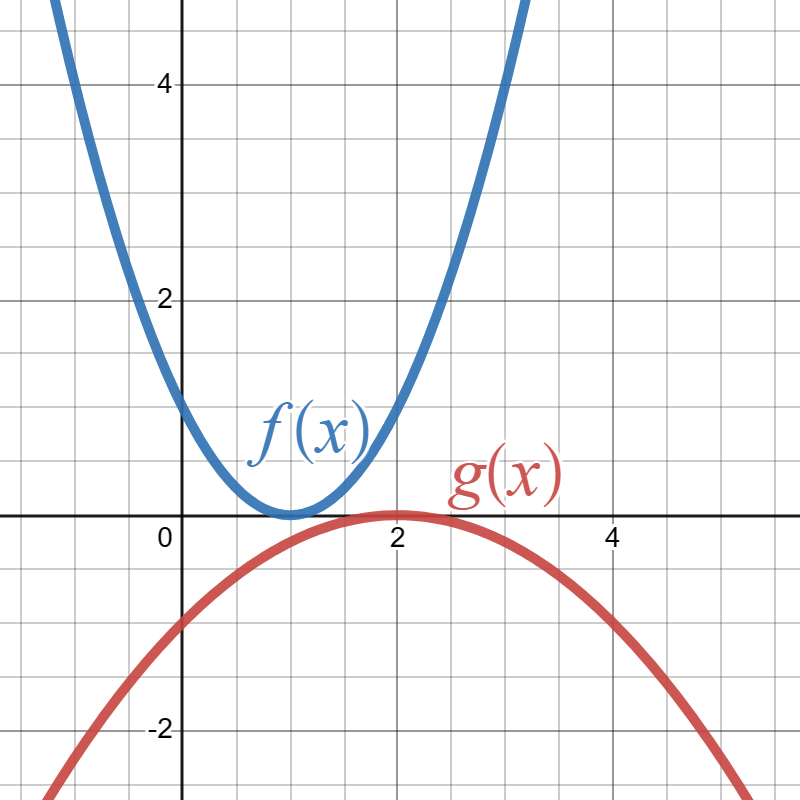
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=-f\left(\frac{1}{2}x\right)\)
22.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
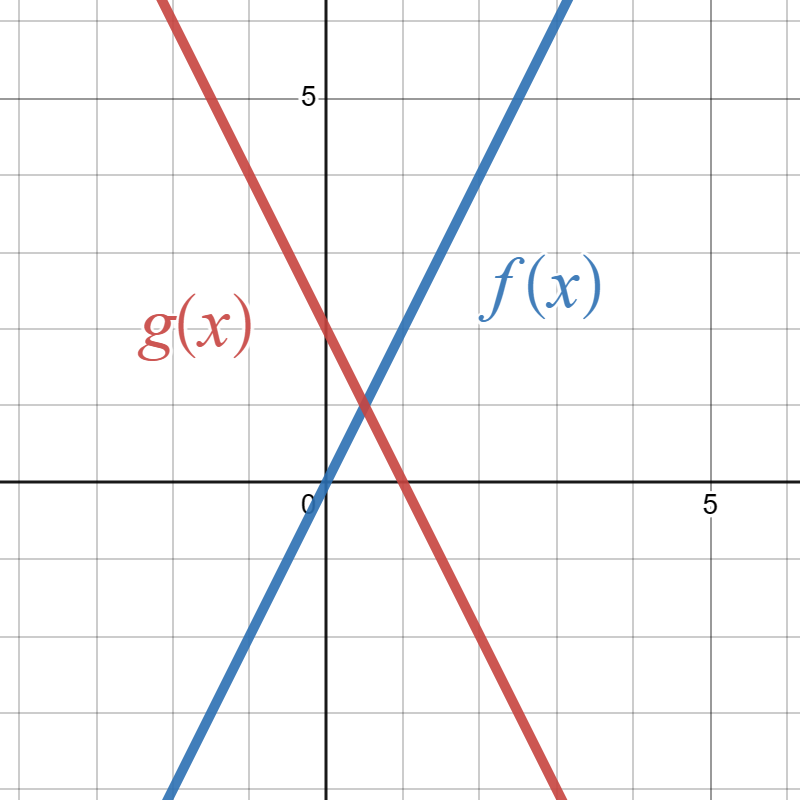
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f\left(-x\right)+2\)