Section 9.6 Combining Transformations
Each of the transformations we've discussed in this chapter have two properties:
The Direction of Transformation: Is it vertial or horizontal?
The Kind of Transformation: Is it a shift, scale, or reflection?
When we are working with multiple transformations at once, those are the two key questions we need to ask. Here is a summary of what we know about each transformation we have talked about:
Fact 9.69. Vertical or Horizontal.
Vertical transformations change the \(y\)-values of the graph, and the formula changes on the outside of the function.
Horizontal transformations change the \(x\)-values of the graph, and the formula changes on the inside of the function.
Fact 9.70. Shift, Scale, or Reflection.
Shift transformations involve adding or subtracting a number in the formula.
Scale transformations involve multiplying or dividing by a positive number in the formula.
Reflection transformations involve multiplying by \(-1\) in the formula.
| Vertical (outside) | Horizontal (inside) | |
| Add | Shift up by \(a\text{:}\) \(f(x)+a\) | Shift left by \(a\text{:}\) \(f(x+a)\) |
| Subtract | Shift down by \(a\text{:}\) \(f(x)-a\) | Shift right by by \(a\text{:}\) \(f(x-a)\) |
| Multiply (\(b\gt 1\)) | Vertical stretch by \(b\text{:}\) \(bf(x)\) | Horizontal squish by \(b\text{:}\) \(f(bx)\) |
| Divide by \(b\gt 1\) | Vertical squish by \(b\text{:}\) \(\frac{1}{b}f(x)\) or \(\frac{f(x)}{b}\) | Horizontal stretch by \(b\text{:}\) \(f\left(\frac{1}{b}x\right)\) or \(f\left(\frac{x}{b}\right)\) |
| Multiply by \(-1\) | Vertical flip: \(-f(x)\) | Horizontal flip: \(f(-x)\) |
Example 9.72.
Suppose \(g(x)=2f(x+3)\) and we want to identify what tranformations took \(f(x)\) to \(g(x)\text{.}\) We see that there are two numbers we need to look at: the \(2\) and the \(3\text{:}\)
In the formula \(g(x)={\color{blue}{2}}f(x+3)\text{,}\) the \(2\) is on the outside of the function, so it's a vertical transformation. Since it's being multiplied, we know that it is a scale. We know from Section 9.3 that a vertical scale by a number greater than \(1\) is a vertical stretch.
In the formula \(g(x)=2f(x+{\color{blue}{3}})\text{,}\) the \(3\) is on the inside of the function, so it's a horizontal transformation. Since it's being added, we know that it is a shift. We know from Section 9.2 that a horizontal shift by a positive number is a horizontal shift to the left.
Therefore, the answer is that there is a vertical stretch by 2 and a horizontal shift left by 3.
Checkpoint 9.73.
Suppose \(g(x)=-f(x-7)\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical reflection and a horizontal shift right by 7.
We see that there are two numbers we need to look at: the \(-1\) and the \(7\text{:}\)
In the formula \(g(x)={\color{blue}{-}}f(x-7)\text{,}\) the \(-1\) is on the outside of the function, so it's a vertical transformation. Since it's multiplying by \(-1\text{,}\) we know that it is vertical reflection.
In the formula \(g(x)=-f(x-{\color{blue}{7}})\text{,}\) the \(7\) is on the inside of the function, so it's a horizontal transformation. Since it's being subtracted, we know that it is a shift. We know from Section 9.2 that a horizontal shift by a negative number is a horizontal shift to the right.
Therefore, the answer is that there is a vertical reflection and a horizontal shift right by 7.
Example 9.74.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
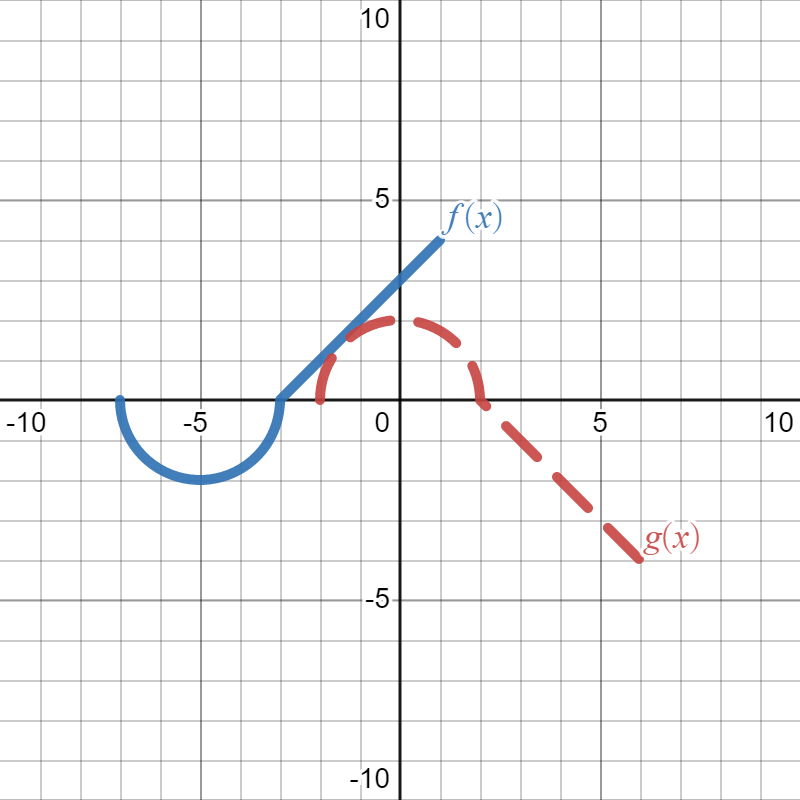
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\text{,}\) but it has been flipped vertically (over the \(x\)-axis) and shifted to the right (in the positive \(x\)-direction) by \(5\text{.}\) The vertical flip means we are multiplying by \(-1\) outside of the function \(f(x)\text{,}\) and the shift to the right means we are subtracting \(5\) from the inside of the function. So, our final answer is \(g(x)=-f\left(x-5\right)\text{.}\)
Checkpoint 9.75.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
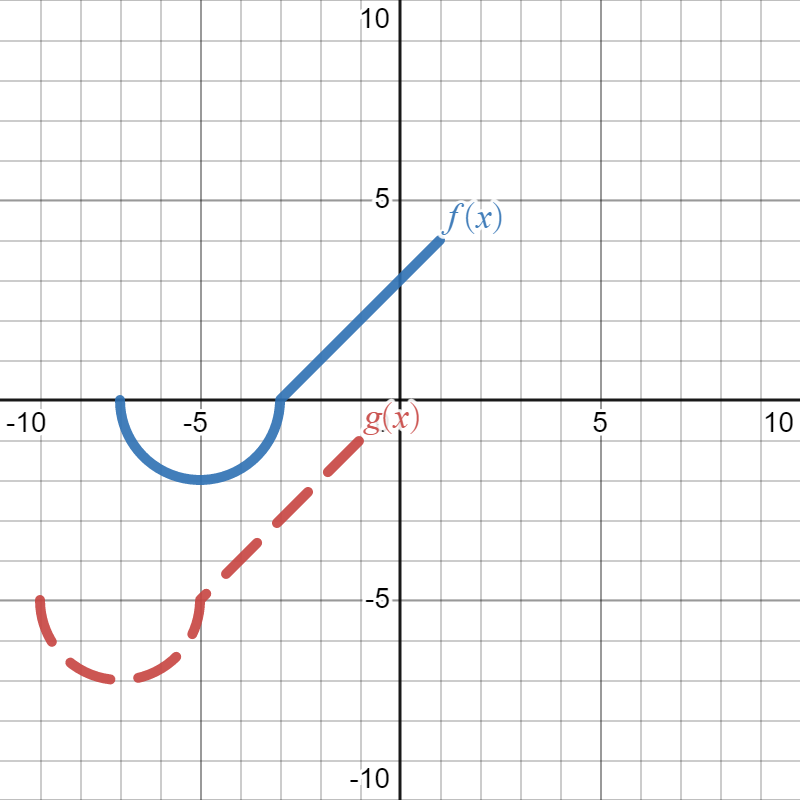
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f\left(x+2\right)-5\)
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\text{,}\) but it has been shifted down by \(5\) and shifted to the left (in the negative \(x\)-direction) by \(2\text{.}\) The vertical shift down means we are subtracting \(5\) from the outside of the function \(f(x)\text{,}\) and the shift to the left means we are adding \(2\) to the inside of the function. So, our final answer is \(g(x)=f\left(x+2\right)-5\text{.}\)
Exercises Practice Problems
1.
Suppose \(g(x)=2f(x-3)\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical stretch by 2 and a horizontal shift right by 3.
2.
Suppose \(g(x)=f(-x)+2\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a horizontal flip and a vertical shift up by 2.
3.
Suppose \(g(x)=-f(x+1)\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical flip and a horizontal shift left by 1.
4.
Suppose \(g(x)=f(\frac{1}{2}x)-4\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a horizontal stretch by 2 and a vertical shift down by 4.
5.
Suppose \(g(x)=f(x-8)+6\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
There is a vertical shift up by 6 and a horizontal shift right by 8.
6.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
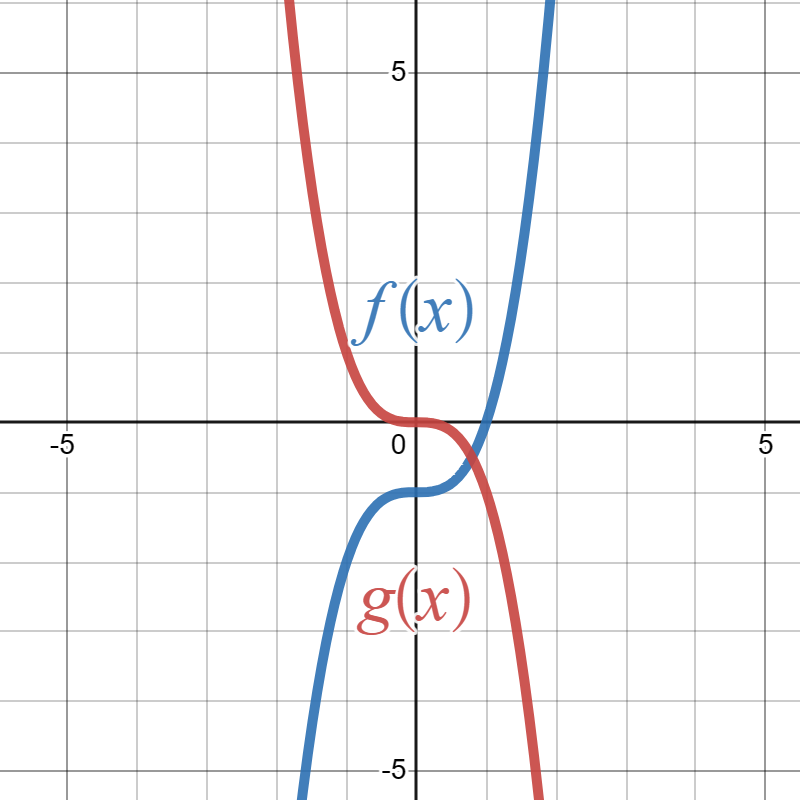
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f\left(-x\right)+1\)
7.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
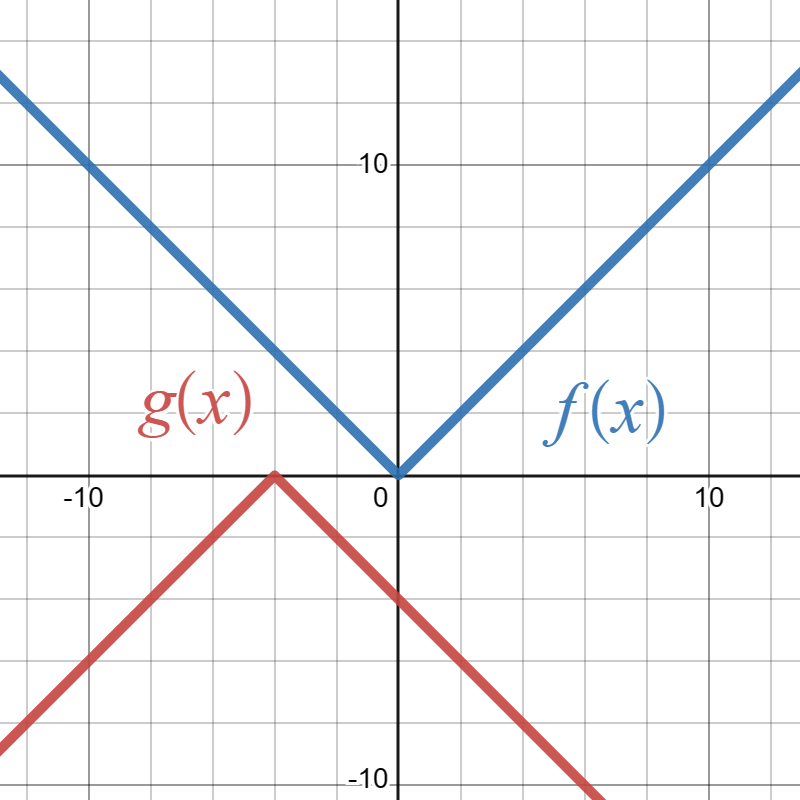
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=-f\left(x+4\right)\)
8.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
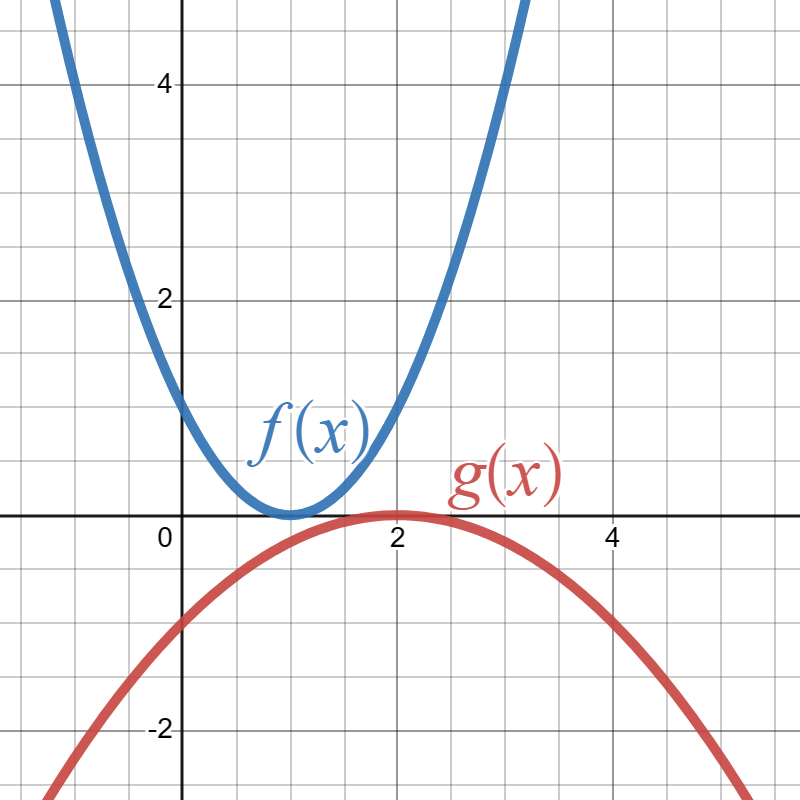
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=-f\left(\frac{1}{2}x\right)\)
9.
Suppose the blue graph below is the graph of \(f(x)\) and the red graph is the graph of \(g(x)\text{:}\)
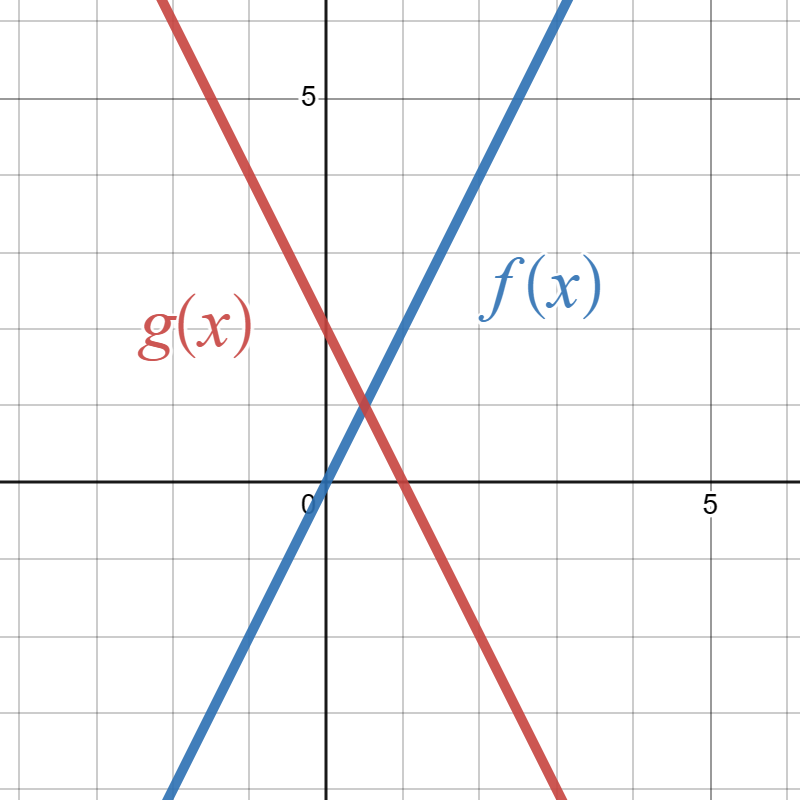
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f\left(-x\right)+2\)